Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

argument nombres complexes

Posté par
ennaji00001 05-02-19 à 13:19

salut tout le monde
s'il vous plait aider moi à calculer sous forme trigonométrique les nombres complexes suivant:
Z1=cosx+i(1+sinx)
Z2=1-cosx-isinx
c'est combien le module et l'argument
merci infiniment

Posté par
Ramanujanre : argument nombres complexes 05-02-19 à 13:28

La module de z_1  est : \sqrt{\cos^2(x) + (1+\sin^2(x))^2

Or 1+sin^2(x)= 2 - cos^2(x)

Donc ...

Posté par
Pirhore : argument nombres complexes 05-02-19 à 13:31

Bonjour,

Ramanujan ton module est faux sous le radical!

Posté par
malou Webmasterre : argument nombres complexes 05-02-19 à 13:48

et en plus d'être faux, je trouve que le chemin proposé est un détour inutile....

Posté par
ennaji00001re : argument nombres complexes 05-02-19 à 13:53

c'est faux Monsieur  et on plus la méthode ne permet pas de déterminer l'argument

Posté par
etniopalre : argument nombres complexes 05-02-19 à 15:04

cos(x) +i ( 1 + sin(x))  = i + exp(ix) = exp(i/2) + exp(ix) = exp(i(/4 + x/2)).( .... )  

Posté par
jsvdbre : argument nombres complexes 05-02-19 à 15:07

Bonjour ennaji00001.

z_1 = \cos(x) + i(\sin(x) +1) = \cos(x) + i\sin(x) + i=e^{ix}+i

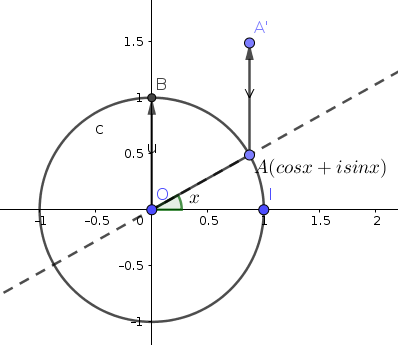
quand x parcourt \R, z_1 parcourt le cercle de centre i et de rayon 1. Il peut donc avoir un argument \theta \in ]0;\pi[.

ennaji00001 @ 05-02-2019 à 13:53

et en plus la méthode ne permet pas de déterminer l'argument

Bah si, précisément c'est la bonne méthode.

|z_1| = \sqrt {\cos^2(x) + (1+\sin(x))^2}=\sqrt{2+2\sin(x)}=\sqrt 2 \sqrt{\sin(x)+1}

On a donc

|z_1| = \sqrt 2 \sqrt{1+\sin(x)}\left(\dfrac{\cos(x)}{\sqrt 2 \sqrt{1+\sin(x)}}+i\dfrac{\sin(x)+1}{\sqrt 2 \sqrt{1+\sin(x)}}\right)=\sqrt 2 \sqrt{1+\sin(x)}\left(\dfrac{\cos(x)}{\sqrt 2 \sqrt{1+\sin(x)}}+i\dfrac{\sqrt{1+\sin(x)}}{\sqrt 2 }\right)

reste à voir que \dfrac{\sqrt{1+\sin(x)}}{\sqrt 2 } =\left|\sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)\right| , mettre le bon intervalle d'étude pour x, étudier la période ...

... et conclure ...

Posté par
malou Webmasterre : argument nombres complexes 05-02-19 à 15:07

un petit regard géométrique

argument nombres complexes

Posté par
etniopalre : argument nombres complexes 05-02-19 à 15:07

Si tu fais un dessin , tu peux trouver module et argument de i + exp(ix)  sans l'astuce que j'ai proposée .

Posté par
malou Webmasterre : argument nombres complexes 05-02-19 à 15:08

quel tir groupé ....

Posté par
jsvdbre : argument nombres complexes 05-02-19 à 15:10

Oui, rien pendant plus d'une heure et soudainement la foudre se déchaîne

Posté par
jsvdbre : argument nombres complexes 05-02-19 à 15:10

Qu'est-ce-qu'on peut être studieux dans nos "foyers" !

Posté par
ennaji00001re : argument nombres complexes 05-02-19 à 15:34

merci Monsieur
pour le module c'est bien mais comment peut on écrire
cos(x)/ (\sqrt{2} .\sqrt{1+sin(x)} sous forme de  cos(y) tel que y est l'argument.
je crois qu'il y a autre chose à faire

Posté par
jsvdbre : argument nombres complexes 05-02-19 à 17:16

Tu trouves un argument via la partie imaginaire.
Et donc tu pourras écrire \dfrac{\cos(x)}{\sqrt{2} .\sqrt{1+\sin(x)}} = \cos(\theta)

Posté par
carpediemre : argument nombres complexes 05-02-19 à 17:33

salut

je pose p = \dfrac {\pi} 2

z = \cos x + i (1 + \sin x) = \cos x + \cos p + i(\sin x + \sin p) = 2\cos \dfrac {x + p} 2 \cos \dfrac {x - p} 2 + i \left( 2 \sin \dfrac {x + p} 2 \cos \dfrac {x - p} 2 \right) = 2 \cos \dfrac {x - p} 2 e^{i\dfrac {x + p} 2}

il reste alors à discuter du signe du coefficient de l'exponentielle ... sachant que -1 = e^{i\pi}

Posté par
carpediemre : argument nombres complexes 05-02-19 à 17:40

je pose x = 2y

z = 1 - \cos x - i \sin x = 2 \sin^2 y - 2i \sin y \cos y = 2 \sin y ( \sin y - i \cos y) = -2i \sin y (\cos y + i \sin y) = ...

sachant que -1 = e^{i\pi}  et  i = e^?

Posté par
etniopalre : argument nombres complexes 05-02-19 à 18:40

Avec ma façon de faire et en utilisant la relation  ( valable pour tout (s , t) ² )  
exp(is) + exp(it) = exp(i(s + t)/2). exp(i(s - t)/2) + exp(i(t - s)/2)  = 2cos((s - t)/2).exp(i(s+t)/2 )   en prenant s =  /2 et t = x  tu obtiens
cos(x) + i(1 + sin(x)) = 2cos(/4 - x/2) . exp(i (/4 + x/2))

Si tu veux  un argument  de  cos(x) + i(1 + sin(x))  ,  il te faudra trouver les x pour lesquels   u(x) :=  cos(/4 - x/2)   est >  0  et  ceux pour lesquels  u(x)  est < 0  .


Posté par
vhamre : argument nombres complexes 05-02-19 à 19:55

Bonsoir,

Pour aller dans le sens de Malou et ouvrir une voie "géométrique" immédiate :
\widehat{BIM'} = \widehat{AOM}  \text{ par translation et }argument(Z1)= \widehat{AOM'}=\dfrac{\pi}{4} + \dfrac{\widehat{AOM}}{2} \text{ par angle inscrit}

L'obtention du module(Z1)=OM' est tout autant immédiat.

argument nombres complexes


Rechercher
Menu
Espace membre
33 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !