Inscription / Connexion Nouveau Sujet
Arguments-Nombre complexe-ensemble de points
Bonjour, j'ai bientôt un contrôle sur cela mais je n'arrive toujours pas à comprendre. Vous pouvez m'aider svp
1)(MA, MB)= 0(pi) on dit que l'ensemble des points est la droite (AB) privé des points A et B
Mon problème ici est que pourquoi c'est toute la droite (AB) , n'est-ce pas si M se trouve entre A et B, l'angle ne vaut plus 0 mais pi. Normalement le segment AB ne devrai pas être exclu
2)(MA,MB)=0(2pi) l'ensemble ici est la droite privé du segment AB
Là j'ai compris mais le bémol c'est qu'il doit y avoir forcément une différence entre 0(pi) et 0(2pi)
princesyb, voici une fiche qui devrait t'aider
![]() Des interprétations géométriques (nombres complexes)
Des interprétations géométriques (nombres complexes)
Ah je comprends donc pourquoi c'est toute la droite et en suivant votre raisonnement pour modulo 2 pi, M occupe les positions par exemple
-40pi,...-2pi,0pi,2pi,4 pi..., 16 pi
Mais j'ai pas compris pourquoi AB est exclu en faisant ce raisonnement
J'ai regardé votre fiche et j'ai tout compris. Mon seul problème c'est avec l'angle 0.
Je comprends tout les autres
Par exemple
C'est le cercle de diamètre AB privé de A et B
Si k=0 on a pi/2
Si k=1 on a 3pi/2
Si k=2 on a 5pi/2 ce qui revient au même pi/2
Si k=3 on a 7pi/2 ce qui revient à ajouter à pi/2, pi (3pi/2 car nombre impairx pi =pi)
Donc c'est l'ensemble du cercle car qu'importe la ou se trouve M, l'angle sera toujours pi/2
Maintenant
C'est le demi cercle de diamètre AB privé de A et B
car à cause de 2pi, M ne pourra jamais aller de l'autre côté du cercle (nombre x pi=0,ca revient donc au même)
Vous avez vu moi j'ai compris pour les autres angles, c'est pour 0 que je n'arrive pas à comprendre, oui je comprends pas le plus simple
Peut être si vous me m'expliquer sous forme de schéma je comprendrao plus facilement
Imagine A, B et M sur une ligne horizontale.
Si M est entre A et B, A à gauche et B à droite,
La demi droite (A,M] part de M est va sur la gauche.
La demi-droite [M,B) part aussi de M mais vers la droite.
C'est pourquoi l'angle vaut alors

Est-ce mieux ainsi?
On distingue deux demi-droites distinctes quand M est entre A et B
Une seule quand M est en dehors.
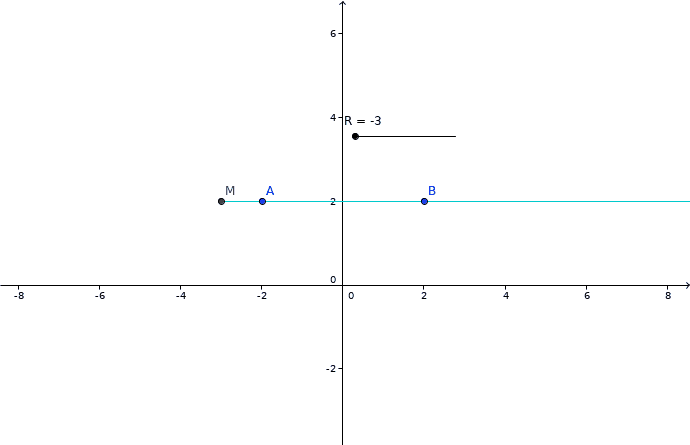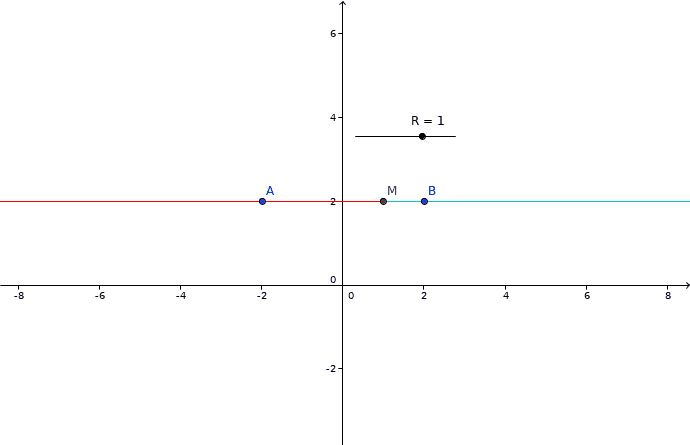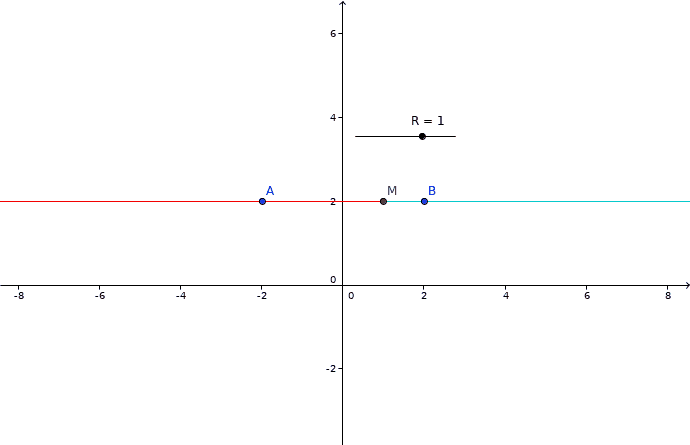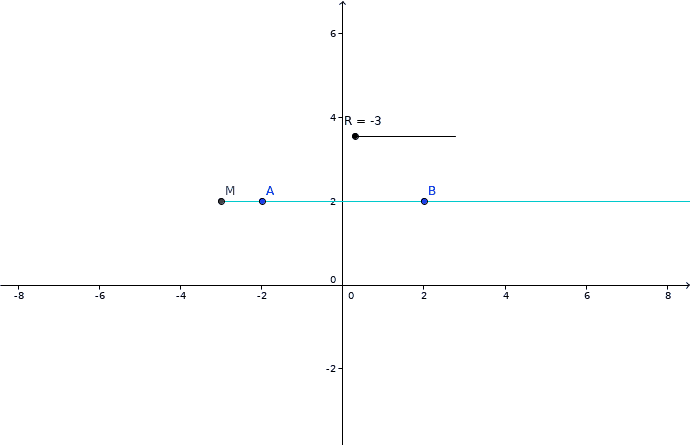
Votre animation est rrs bien fait et tout, ça permet de vite comprendre
Vous pouvez le faire pour 0 modulo 2 pi s'il vous plaît. Je veux savoir pourquoi M ne parcoure pas le segment AB
mets un point M n'importe où entre A et B, sur le segments
dessine les vecteurs MA et MB
mets toi sur le vecteur MA
et tourne pour arriver sur le vecteur MB
quel angle as-tu fait ?
si ça fait pi, c'est que tu as un angle plat
donc ça ne peut jamais faire 0 (à un tour complet près)
donc tout ce qui est entre A et B doit être enlevé si tu veux 0 à 1 ou plusieurs tours près
vois -tu ?
Je viens tout juste de comprendre. J'ai essayé de visualiser tous dans ma tête et j'ai enfin tout saisi
Merci pour vous tous de votre aide précieuse


