Inscription / Connexion Nouveau Sujet
barycentre d'un système pondéré de points
Bonjour,
J'ai un dm de maths à faire sur les barycentres, or je n'ai jamais entendu parler de ça et je n'ai pas de cours dessus...voilà l'énoncé:
SUJET:
A) AVEC DEUX POINTS
On considère une balance représentée par le segment [AB] de longueur 10cm et on suspend une masse mA = 2kg en A et une masse mB = 6kg en B.
On cherche le point d'équilibre G de ce système.
La deuxième loi de Newton appliquée à un solide en rotation permet d'écrire la relation : mAGA + mBGB = 0. On dit que le point G est le barycentre du système de points pondérés {(A; mA), (B; mB)}, où les masses sont les coefficients affectés aux points A et B.
1) Dans l'exemple donné,
a) Exprimer, à l'aide de la relation de Chasles, le vecteur AG en fonction du vecteir AB.
b) Construire le point G
2° De manière générale, exprimer le vecteur AG en fonction du vecteur AB
3) En mathématiques, dans le système {(A; a), (B; b)}, les coefficients a et b peuvent être négatifs. Dans le cas où a+b= 0 que se passe-t-il pour le point G,
En déduire une condition d'existence du barycentre.
B) AVEC PLUSIEURS POINTS
De même, dire que G est le barycentre du système {(A; a), (B; b), (C; c)} signifie que aGA + bGB + cGC = 0
1) On étudie le cas particulier du barycentre du système {(A; 1), (B; 1), (C; 1)}. On note I le milieu de [BC]
a) Exprimer le vecteur AG en fonction du vecteur AI. En déduire que le point G appartient à la médiane (AI).
b) Démontrer que les trois médianes du triangle sont concourantes en G.
2) De manière générale, on note H le barycentre du système {(B; b), C; c)} quand il existe.
a) Démontrer que G est aussi le barycentre du système {(A; a), (H; b+c)}.
3) Construire le barycentre du système {(A; 1); (B; 2), (C; 3)}.
4) Construire le barycentre du système {(A;-1), (B; 3), (C; 2), (D; 1)}
Merci d'avance pour votre aide 
Bonjour jeansch,
cette fiche pourra t'aider : ![]() cours sur les barycentres
cours sur les barycentres
dire que G est le barycentre du système {(A; a), (B; b), (C; c)} signifie que aGA + bGB + cGC = 0
Ces phrases peuvent paraître compliquées, abstraites.
Expliqué comme ça, il faut du courage pour comprendre.
C'est quoi un barycentre, concrètement.
Imagine que tu as des boules de pétanque, ou plus généralement des masses assez lourdes, de poids éventuellement différents.
Donc par exemple 2 boules de 1 kilo, et une autre de 5 kilos.
Ces boules sont reliées entre elles par une petite structure en bois, de poids négligeable.
Donc par exemple, les 3 boules sont aux 3 sommets d'un triangle équilatéral.
Et on cherche le centre de gravité de cet assemblage.
Intuitivement, ce centre de gravité va être assez près de la boule la plus lourde.....
C'est exactement cette relation qui est écrite dans cette formule aGA+bGB+cGC=0
Barycentre=centre de gravité, dans le cas général.
Isobarycentre=Centre de gravité, dans le cas particulier où toutes les boules ont le même poids .... tout simplement parce que le préfixe grec iso signifie identique, égal...
1) Pour la relation de Chasles, je dirais que :
AG = AB - GB, soit :
AG = AB + BG
1b) /
2) Pour exprimer de manière générale le vecteur AG en fonction de AB, je fais :
AG= xAB + yBG ?
2GA + 6GB = 0
2GA = -6GB
2GA = -6(GA + AB)
2GA = -6GA - 6AB
8GA = -6AB
4GA = -3AB
GA = -3/4AB
AG= 3/4 AB
Est ce correct ?
Concernant la question 1b) Construire le point G
Il me suffit de schématiser la situation et de le placer aux 3/4 d'AG?
Oui
Non. Comment pouvez-vous placer G aux trois quarts de AG ?
Faites attention, AB alors cela fonctionne
oui, en effet, merci de m'avoir rectifié.
Pour la question 2) De manière générale, exprimer le vecteur AG en fonction du vecteur AB
J'écris simplement : AG=xAB ?
Ce sera la fin de la démonstration, mais avant il faudra dire ce que vaut ce
Vous faites comme précédemment avec 2 et 6, mais cette fois avec et
À la fin vous pourrez vérifier en donnant à la valeur 2 et à
la valeur 6
aGA = bGB = 0
aGA = -bGB
aGA = -b(GA + AB)
aGA = -bGA - bAB
a+bGA = -bAB
GA = -b/a+b x AB
AG = b/a+b x AB
Si je vérifie avec 2 et 6, j'obtiens bien, 6/2+6AB, soit 6/8AB=3/4AB
3) Si a+b = 0, alors on ne peut pas définir le barycentre du système. On peut donc en déduire que pour que pour que le point G existe, il faut que a +b ne soit pas égal à 0 ?
Une petite erreur au début, il fallait appuyer aussi sur Maj pour avoir + et non =
Il serait intéressant de voir ce qui se passe, si
on a alors A=B ce qui est faux puisque A et B sont distincts
en effet je me suis trompé, je voulais bien mettre un "+"
Je ne comprends pas là où vous voulez en venir avec GA - GB = 0...
On cherche un point G vérifiant: aGA + bGB = 0
aGA + bGB = aGA + b(GA + AB)
aGA + bGB = (a + b)GA + bAB
aGA + bGB = 0 ??
Que voulez-vous faire ?
Si vous êtes dans le cas alors
et par suite on peut prendre
On aurait A=B, mais comme ils sont distincts ce n'est pas possible
ah mais oui! J'ai cherché trop compliqué pour le coup
B) AVEC PLUSIEURS POINTS
De même, dire que G est le barycentre du système {(A; a), (B; b), (C; c)} signifie que aGA + bGB + cGC = 0
1) On étudie le cas particulier du barycentre du système {(A; 1), (B; 1), (C; 1)}. On note I le milieu de [BC]
a) Exprimer le vecteur AG en fonction du vecteur AI. En déduire que le point G appartient à la médiane (AI).
Pour cette question j'ai trouvé :
1GA + 1GB + 1GC = 0
1GA +1(GI+IB) +1(GI+IC)=0
1GA + 1GI -1/2BC + 1GI +1/2BC =0
1GA + 1GI + 1GI = 0
1GA + 2GI =0
1GA + 2(GA+AI) =0
1GA + 2GA + 2AI = 0
3GA =-2AI
-3AG = -2AI
Le point G appartient à la médiane AI car on a -3AG=-2AI
On peut faire plus simple
G isobarycentre de A B et C
I milieu de [BC]
On remarque au passage que I est l'isobarycentre de B et C
Donc
Remarque : Ceci suffisait pour dire que G appartenait à la médiane (AI)
On peut aussi remarquer que le barycentre total n'a pas changé en remplaçant deux points par leur barycentre affecté de la somme des coefficients.
d'où
b on réitère la démarche en changeant de milieu
Vous avez montré que G appartenait à la médiane (AI) maintenant on va montrer que G appartient à la médiane (BJ)
puis, que G appartient à la médiane (CK) C'est la même démonstration
J milieu de [AC]
Donc
G appartient à la médiane (BJ)
ou si vous préférez on tourne A devient B, B devient C, C devient A
J milieu de [CA]
On remarque au passage que I est l'isobarycentre de C et A
Donc
G appartenait à la médiane (BJ)
donc pour montrer que G appartient à la médiane CK, on fait :
GA + GB + GC = 0
GK + KA + GB + GK + KC = 0
K milieu de [AB] KC + KA = 0
donc GB + 2GK = 0
G appartient à la médiane (CK)
Avez-vous réalisé une figure ? J'ai l'impression que vous vous perdez dans les points
K milieu de [AB]
Donc
G appartient à la médiane (CK)
G appartenant aux trois médianes, elles sont donc concourantes
j'ai fait une figure mais me suis complètement emmêlé…
Pour la question :
2) De manière générale, on note H le barycentre du système {(B; b), C; c)} quand il existe.
a) Démontrer que G est aussi le barycentre du système {(A; a), (H; b+c)}.
J'ai trouvé :
On a G barycentre de {(A; a), (B; b), (C; c)} donc aGA + bGB + cGC = 0
On a H barycentre de {(B; b), (C; c)} soit bKB+ cKC = 0
Comme H barycentre de {(B; b), (C; c)}, on a bGB + cGC = (b +c)GH donc, en remplaçant, on a :
(b+c)GH =cGC =0
C'était bien parti
G barycentre de
traduction
On fait intervenir le point H
on simplifie
On sait que H est le barycentre de donc
Il en résulte
traduction G est le barycentre de (A, a) et de (H, b+c). Et c'est tout
Que vient faire K ici ? Erreur de frappe
On remplace dans l'égalité de départ
merci de m'avoir éclairé
3) Construire le barycentre du système {(A; 1); (B; 2), (C; 3)}.
1GA + 2GB + 3GC = 0
considérons le point H barycentre de A(1) B(2) C(3), on a donc :
1HA + 2HB + 3HC = 0
je suis bloquée à cette étape, je ne sais pas ce que je dois faire après
Prendre exemple sur ce qui précède
les barycentres partiels existent tous
Si vous avez remarqué que si les coefficients étaient les mêmes, pour un barycentre de 2 points, alors c'était le milieu
On va donc choisir H barycentre de ainsi G sera le barycentre de (H,3) (C,3)
On a vu, lors des premières questions en adaptant, que
On construit donc H (c'est le centre de gravité du triangle ABC) Puis G qui est le milieu de [HC]
Remarque : En bref, vous avez donné deux noms au barycentre des 3 points H et G puisque vous écrivez la même relation vectorielle.
Il faut passer par des barycentres partiels.
Quant à la dernière question G barycentre de {(A;-1), (B; 3), (C; 2), (D; 1)}
on peut construire H, le barycentre de
puis K le barycentre de
enfin G le barycentre de
N.B. Ce n'est qu'une proposition, d'ailleurs il y a une construction plus astucieuse
Bonjour
Je me permet d'intervenir:as tu compris la difference d'utilisation des deux formules de definition du barycentre?
La relation de construction permet de construire le barycentre global G à partir d'un barycentre partiel et d'un vecteur connu
par exemple HG= k HC
Pour aboutir à celà c'est la formule d'associativité qui te sert:
(aGA+bGB)+cGC=0 sachant que aGA+bGB = (a+b)GK
et mon vecteur connu c'est donc AH = 2/3 AB ?
cette relation te permet de construire H et tu remplaces ensuite dans la definition globale de G comme je viens de te l'indiquer
Je garde les mêmes notations que précédemment
G barycentre total et H barycentre partiel
G est le barycentre de (A, 1) (B, 2) et (C, 3)
Traduction On veut construire G vérifiant cette égalité
On introduit H barycentre de et
Donc Cette relation permet de construire le point H
On revient à G. On peut donc dire que G est le barycentre de H affecté de 1+2 =3 et de C affecté de 3
soit vectoriellement ou encore
Cette dernière égalité caractérise le milieu d'un segment, ici le segment [GC]
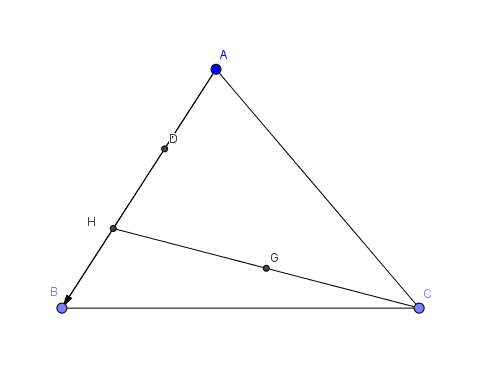
Le point D est juste là pour montrer que H est au 2/3 de [AB]
pardon ! j'ai mis K au lieu de H!!! Je t'embrouille....
D'autre part je vois qu'hekla est revenu alors je le laisse reprendre le relai
Vous mélangez un peu
Quel est l'intérêt d'écrire que
La relation vectorielle sert à placer le barycentre partiel. Que vous partiez de A ou de B ne change rien
Vous ne faites pas les présentations pourquoi revenir à a et b ?
La dernière ligne n'est guère compréhensible
Que vient faire ce 2/3 ce n'est pas un poids affecté à un point
Reprenons
première étape : barycentre de deux points
G barycentre de (A, a) (B, b)
il existe si la somme des coefficients est non nulle et pour le placer on a démontré la relation vectorielle
\vec{AG}=\dfrac{b}{a+b}\vec{AB}
deuxième étape : barycentre de 3 points
Notation
G barycentre de (A, a) (B, b) (C, c)
H barycentre partiel de (B, b) (C, c)
Démonstration
G barycentre de
traduction
On fait intervenir le point H
on simplifie
On sait que H est le barycentre de donc
Il en résulte
traduction G est le barycentre de (A, a) et de (H, b+c).
Troisième étape Application construction de G
Notation
G barycentre de (A, 1) (B, 2) (C, 3)
H barycentre partiel de (A, 1) (B, 2)
D'après les questions précédentes
étape intermédiaire
G est le barycentre de (H, 3) et de (C, 3)
Conclusion G est le milieu La relation vectorielle est caractéristique du milieu d'un segment
ou on reprend
Ce qui donne aussi le milieu de [HC]
Vous disiez être perdu donc j'ai tout repris
pour la 3
G barycentre de (A, 1) (B, 2) (C, 3)
Considérons H le barycentre de il est tel que
G est le barycentre de (H, 3) et de (C, 3)
G est le milieu de [HC]


