- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Barycentre et produit scalaire
Bonjour. J'ai un exercice à rendre jeudi mais je n'arrive pas à le faire.
Pourriez-vous m'expliquer svp?
Voici l'énoncé: (il y a des parties photocopiées, car je ne sais pas comment faire les signes des vecteurs, désolées):
Soit ABC un triangle tel que AB=4, AC=3 et BC=5. On note G le barycentre des points pondérés (A ;5), (B ;3) et (C ;4) et on cherche à montrer que G est le centre du cercle inscrit dans le triangle ABC. Pour le dessin, l'unité graphique est de 2cm.
I : 1.a. Justifiez le fait que le point G est à l'intérieur du triangle ABC.
b. Construisez les barycentres A' de (B ;3) et (C ;4) ; B' de (A ;5) et (C ;4) ; C' de (A ;5) et (B ;3). J'ai réussi à le faire.
c. Justifiez l'affirmation suivante : G est le point de concours des droites (AA'), (BB') et (CC').
2 et 3: cf image
4. On note H, K et L les projetés orthogonaux de G sur les droites (AC),(AB et (BC) respectivement.
a. Déduisez de la question 3a, que AK=1 et AH=1, puis montrez que GH=GK=1.
b. Montrez, en utilisant 3.B., que CG.BC=-10. Calculez CL puis GL.
Concluez en justifiant le fait que G est le centre du cercle inscrit dans ABC.
Merci par avance.
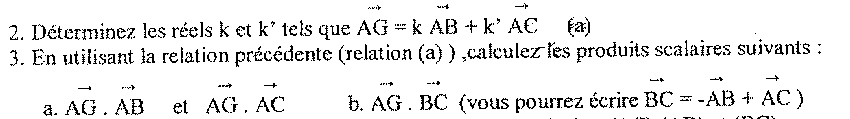
1. G est barycentre des points C(4) et H(9), avec H barycentre des points a(4) et B(5) ..ok??
OU ce trouve H par rapport a A et B
Désolée, je ne vois pas comment tu trouves ça 


