- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Barycentre et produit scalaire
Bonjour à tous !
Voilà je suis en terminale S, et j'ai commencé mon Dm, mais je bloque sur la fin.
Dans la partie 3, la question b, ça commence à coincer :
J'arrive à  .
.  = -4 mais il me faudrait
= -4 mais il me faudrait  .
.  = -4
= -4
Et pour la suite, j'aurais besoin de pistes si c'est possible, parce que je ne comprends pas l'énoncé parfaitement.
En attente de vos réponses, Merci bien .
Ps: ci joint l'énoncé et la figure !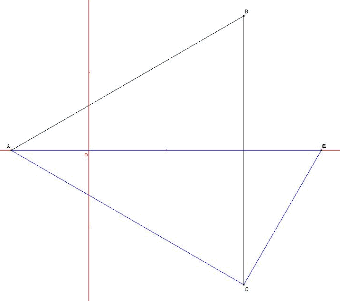
édit Océane : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum
Avec un repère orthonormal direct (O,u,v)
Partie 1:
Pour tout complexe z, on pose f(z)= 2z^3-6z^2+6z+14
a. Calculer f(-1)
b. Déterminer un polynôme Q du seconde degré tel que pour tout complexe z: f(z) = (z+1)* Q(z)
c. Résoudre dans  l'équation f(z)=0
l'équation f(z)=0
Partie 2:
On désigne par A,B,C,G les points d'affixes respectives:
Za=-1 ; Zb=2+i 3 ; Zc = 2-i
3 ; Zc = 2-i 3 et Zg=3
3 et Zg=3
a.Placer A,B,C et G
b. Nature de ABC ?
c. Calculer un argument de (Za-Zc)/(Zg-Zc). En déduire la nature de GAC.
Partie 3:
Soit (E) l'ensemble des ponts M du plan tels que: (-MA +2MB+ 2MC) . CG = 12 (relation 1)
a. Montrer que G est la barycentre de {(A,-1)(B,2)(C,2)}
b. Montrer que la relation (1) est équivalente à (vecteurs): GM.GC=-4 (relation 2)
c. Vérifier que A appartient à (E)
d. Montrer que la relation (2) est équivalente à (vecteurs) AM.GC = 0
e. En déduire l'ensemble (E) et le tracer .
Oui j'ai vérifié à plusieurs reprises, c'est pour cela que ça m'intriguait.
Par ailleurs, auriez-vous des pistes, ou pourriez-vous m'éclairer sur les questions suivantes ? (des pistes SVP)
d. Montrer que la relation (2) est équivalente à (vecteurs) AM.GC = 0
introduis le point A dans la relation 2 corrigée( 4 à la place de-4)
Si(vecteurs) AM.GC = 0 alors (AM) et (CG) sont.....
Donc... (AM) et (GC) sont perpendiculaires,
et l'ensemble (E) est la droite (AC).
Si c'est cela j'ai fini. Et je vous remercie de votre aide 


