- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Bonjour, problème avec un cube
Bonjour,
Voilà je bloque dans mon exo.
Lorsque je met  XX, cela veut dire que c'est le vecteur XX (désolé je ne sais pas faire les vecteurs)
XX, cela veut dire que c'est le vecteur XX (désolé je ne sais pas faire les vecteurs)
Sachant que:
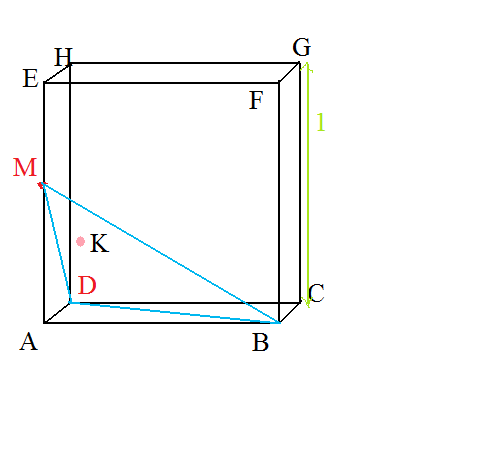
ABCDEFGH est un cube d'arête 1
 AM = (1/a) *
AM = (1/a) *  AE
AE
K est le barycentre des points (M,a2) ; (B,1) ; (D,1)
 BK.
BK. MD = 0
MD = 0
 DK.
DK. MB = 0
MB = 0
K est l'orthocentre du triangle BDM
 AK.
AK. MB = 0
MB = 0
 AK.
AK. MD = 0
MD = 0
Le triangle BDM est isocèle en M et a une aire A= ( (a2+2)) / (2a)
(a2+2)) / (2a)
La question où je bloque est la suivante: Déterminer le a (strictement positif) tel que A=1. Déterminer la distance AK dans ce cas.
J'ai trouvé que a=  (2/3) ( à vérifier on sait jamais)
(2/3) ( à vérifier on sait jamais)
Mais je ne sais pas comment trouver la distance AK dans ce cas.
Merci d'avance pour votre aide.
Bonne soirée
Houla je n'ai pas fait le calcul  .
.
Je peux juste dire que pour a c'est bon.
Mais je vais faire le calcul....bouges pas 
J'aimerais savoir, au début, pour calculer AK, j'avais utilisé de fait que  AK.
AK. MB et là j'avais trouvé que AK=0. Pourquoi cette façon ne marchait pas ?
MB et là j'avais trouvé que AK=0. Pourquoi cette façon ne marchait pas ?

Jamais vu cette égalité, en fait si on fait les calculs ton égalité entraine :
ça me parait vraiment bizarre  car alors deux vecteurs orthogonaux peuvent avoir un produit scalaire non-nul.
car alors deux vecteurs orthogonaux peuvent avoir un produit scalaire non-nul.
Voilà un lien sur le produit scalaire dans l'espace où on trouve les différentes expressions du produits scalaire dont celle avec cosinus : ![]()
J'ai compris, sur mon livre, en effet je trouve celle avec le cosinus, mais je pas la même que celle du lien avec le 0.5*.
J'ai trouvé mon erreur, U.V= 0.5*( (norme U)2 + (norme V)2 - (norme  U-
U- V)2 et non pas (norme U - norme V )2
V)2 et non pas (norme U - norme V )2
Par contre je ne sais pas si ça fait pareil que celle sur le lien que tu m'as donné.
Avec la formule avec le cos, la valeur de AK n'as pas d'importence, donc elle ne peut pas nous aider pour vérifier
Elles sont peut-être équivalentes.....mais bon tu as celle du cosinus, c'est celle qui est le plus utilisée.



