Inscription / Connexion Nouveau Sujet
Calcul Aire entre 3 courbes
Salut on me demande de calculer l'air comprise entre les fonctions Y= 3x-2 et X=(Y-1)^2
Dans la deuxieme fonction qui n'en est plus une, en isolant Y on obtient, Y=Racine(X)+1 ou Y=1-Racine(x)
Voici le graph obtenu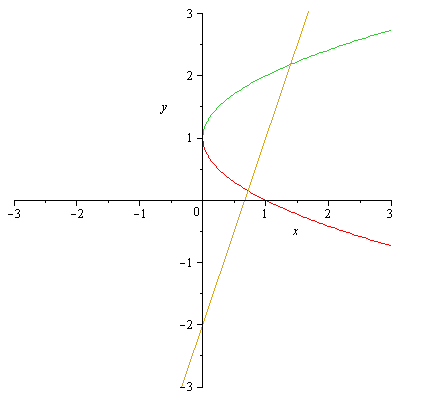
Pour trouver les points d'intersection j'ai fait 3x-2=Racine(X)+1 ou 3x-2=1-Racine(X)et ils sont bons
Maintenant pour le calcul de l'air entre les 3 courbes (ils précisent qu'ils veulent voir une seule intégrale) j'ai fait:
Integrale((Racine(X)+1) - (1-Racine(X))- (3x-2)), ;es bornes etant les deux points trouvés plutot.
Est ce correcte ? Qu'est ce qui determine l'ordre dans la soustraction ?
édit Océane : forum modifié
* Océane > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois triceratops
, merci d'en faire autant la prochaine fois triceratops  *
*
Salut on me demande de calculer l'air comprise entre les fonctions Y= 3x-2 et X=(Y-1)^2
Dans la deuxieme fonction qui n'en est plus une, en isolant Y on obtient, Y=Racine(X)+1 ou Y=1-Racine(x)
Voici le graph obtenu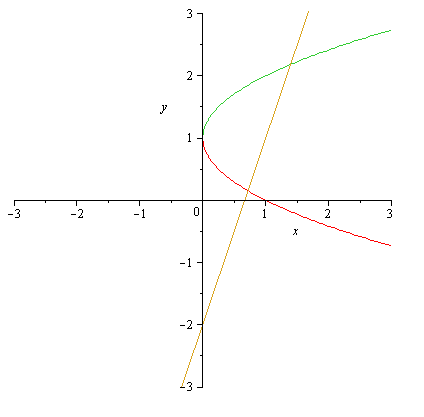
Pour trouver les points d'intersection j'ai fait 3x-2=Racine(X)+1 ou 3x-2=1-Racine(X)et ils sont bons
Maintenant pour le calcul de l'air entre les 3 courbes (ils précisent qu'ils veulent voir une seule intégrale) j'ai fait:
Integrale((Racine(X)+1) - (1-Racine(X))- (3x-2)), ;es bornes etant les deux points trouvés plutot.
Est ce correcte ? Qu'est ce qui determine l'ordre dans la soustraction ?
*** message déplacé ***
* Océane > le multi-post n'est pas toléré sur le forum ! *
* Océane > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois triceratops
, merci d'en faire autant la prochaine fois triceratops  *
*
Bonsoir triceratops,
Tu as l'air de rapporter cette surface en référence à l'axe des abscisses.
Mais il est plus simple de le faire par rapport à l'axe des ordonnées.
Les bornes a et b en y se trouvent en résolvant le système des deux équations :
.
L'aire se calculera par :
Bonsoir triceratops
Je t'ai répondu ici ![]() Calcul Aire entre 3 courbes
Calcul Aire entre 3 courbes
Attention, le multipost est interdit et tu risques une amende !
Probablement bénéficieras-tu du fait que tu viens de t'inscrire...
Et... bienvenue sur l'

*** message déplacé ***
D'abord merci pour ta réponse, ensuite pourquoi est ce que c'est ((y+2)/3)-(y-1)^2 et non (y-1)^2 - ((y+2)/3) ?
Penche ta tête sur la droite et regarde la figure...
La droite est alors "au-dessus" de la parabole.
Ah ok tu integre par rapport a y alors l'axe Y est devenu en quelaue sorte notre ancien axe X.
Salut désolé, c'est juste que je ne savais pas qui étudiait cette branche des maths en france.
*** message déplacé ***
Ne t'inquiète pas trop.
J'ai demandé à un modérateur de déplacer ce topic.
Tout ce que j'espère, c'est que tu ne seras pas sanctionné.
Espérons en sa clémence puisque tu viens d'arriver sur l'île 
*** message déplacé ***
C'est bien ce que j'ai obtenu, désolé de demander encore de l'aide mais là il me demande de calculer le volume de révolution de la région autour de l'axe des x et autour de l'axe de x=3, je nage completement, je ne sais pas si je dois utiliser la méthode des disques ou celle des tubes, pourriez vous m'aider svp ?
Voici ce que je te propose.
Les équations des 3 courbes sont données par
Le volume de révolution engendré par la rotation de la région autour de l'axe des x pourrait se calculer par la méthode des cylindres.
où les bornes sont celles que tu as trouvées (comme tu le dis dans ton premier post de 21h36). J'ai arrondi ces bornes.
Le volume de révolution engendré par la rotation de la région autour de l'axe dont l'équation est x=3 pourrait se calculer par la méthode des tubes.
.
Non, ce n'est pas normal qu'un volume soit négatif.
J'ai machinalement pris « (x-3) » comme étant le rayon de la base du cylindre. 
Tu comprends qu'il s'agit plutôt de (3-x) puisque l'axe de rotation se trouve à droite du graphique.
Les valeurs de x variant de 0 à 1,39 rendraient x-3 négatifs, ce qui n'est pas acceptable comme valeurs des rayons…
Deux solutions se proposent à toi.
Ou bien tu prends la valeur absolue de ton résultat
.
Ce n'est pas très « joli » comme écriture
Ou bien tu modifies le calcul en écrivant ceci :
Le volume du solide est environ égal à 20,56u³.

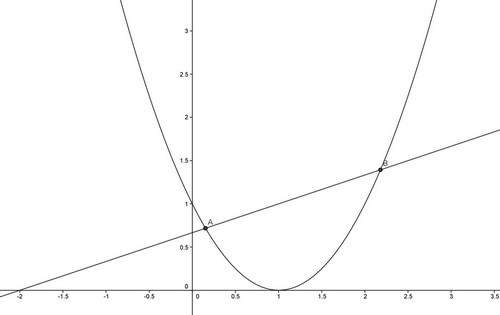

 analyse en post-bac
analyse en post-bac