- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
calcul d'une intégrale par la méthode des résidus
salut
j'ai un problème avec le calcul de lintegrale de -infini jusqu'à +infini de Exp[ax]/(1+Exp[x]) pour 0<a<1 j'ai l'habitude de faire cette opération sur un contour circulaire mais dans ce cas il faut passer par un rectangle .
j'ai fait des recherches mais je n'ai rien trouvé, s'il vous plait si vous avez au moins une idée
merci
Bonjour.
Il faut effectivement utiliser un contour en forme de rectangle.
Je te propose d'intégrer la fonction le long du contour qui délimite le rectangle de sommets
,
,
et
.
C'est relativement le même principe.
Le rectangle choisi sera de longueur 2R centré en 0 (ce sera le chemin paramétré  R).
R).
Tu calcule l'intégrale sur  R par la methode des residus ensuite tu divise ton integrale en 2parties:
R par la methode des residus ensuite tu divise ton integrale en 2parties:
la 1er de -R vers R et la seconde entre 0 et  (utilise le chemin
(utilise le chemin  R).
R).
La fonction entre -R et R sera ta fonction d'origine.
Te reste plus qu'a faire tendre R vers l'infini et calculer ton integrale sur  .
.
j'espère que c'est bon
d'accord merci mais je n'arrive pas à distinguer à quel type elle appartient alors comment intégrer cette dernière (avec z)?
Comment ça quelle type??
La fonction est sur  .
.
La methode des residus consiste a envoyer ta fonction sur  pour pouvoir la resoudre sur
pour pouvoir la resoudre sur  .
.
Le rectangle que tu utiliseras et sur  ²(
²( ) avec l'axe des abssisses qui represente
) avec l'axe des abssisses qui represente  .
.
dans mon cours les intégrales à calculer par résidus sont de 5 formes, une d'elle avec les bornes infinies sont f(x)Exp(ix) tel que f holomorphe sur sur y>=0 , je pense c'est la bonne?
Pas vraiment ...
On n'est pas en présence d'une forme "canonique" d'intégrale, donc je pense pas que celle-ci figure dans ton cours.
On te propose juste d'appliquer le théorème des résidus à la fonction et au contour que je t'ai proposé dans mon message de 15:55.
Dans ton cour, les formes dont tu fais allusion sont je pense les lemmes de Jordan. Mais dans cet exemple, tu n'a pas besoin de les utiliser.
Il te suffit d'appliquer le th des résidus sur un chemin rectangulaire en utilisant la fonction que ta proposé Arkhnor sur 
j'ai utilisé cette formule donnée comme étant le théorème des résidus , le problème persiste parcequ'en l'employant je me trouve obligé de faire un calcul énorme et ça revien a integrer la fonction normalement terrible!
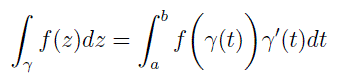
Dans le contour que je t'ai proposé, il y a 4 segments.
Il faut les regarder un par un.
Il n'y a aucun calcul explicite d'intégrale à faire.
Les intégrales sur les deux segments horizontaux vont contribuer à l'intégrale que l'on cherche à calculer, et les intégrales sur les deux segments verticaux tendent vers 0 lorsque R tend vers l'infini. (à démontrer à l'aide de majorations élémentaires sur les intégrales)
Au passage, la formule que tu donnes est fausse, mais ça vient probablement du fait que tu n'as pas remarqué que l'intégrale sur le segment horizontal du haut contribue à la valeur de l'intégrale !

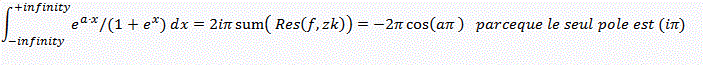

 analyse complexe en post-bac
analyse complexe en post-bac