Inscription / Connexion Nouveau Sujet
Comparaison de courbe Parabolique
Bonjour à tous
je bloque sur un exo le voici :
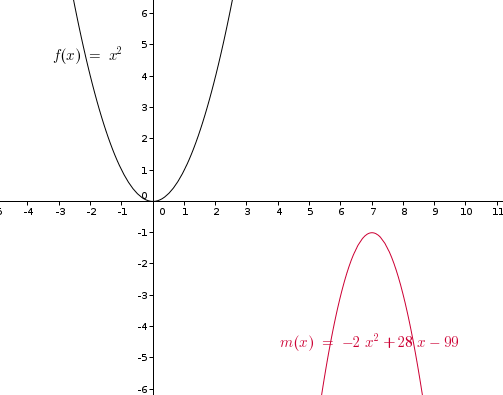
La 1er question me demande de tracer 6 fonctions avec GeoGebra, dont nous avons les équations de droite cela est fait : http://www.hostingpics.net/viewer.php?id=565590maths.jpg
après je dois répondre à des questions les voici :
1. point commun de ces courbes, expliquez
Ce sont toutes des paraboles, cela s'explique car l'équation de droite contient toujours x²
2. Factoriser g(x). Comment obtenir les courbes g et h en fonction de celle de f
g(x) = x² - 10 + 25
g(x) = (x-5)²
Mais la je n'arrive pas à répondre à la deuxième partie, j'ai demander à mon prof, il m'as dis qu'il fallait Utiliser des termes comme translation symétrie etc, mais je ne comprend pas.
après autre question où je bloque :
du même genre, comment obtenir les courbes de k,l et m en fonction de la courbe de f
et, Quel rôle joue le coefficient 3 pour la courbe f ? 

merci d'avance pour tout aide éventuelle
Ce sont toutes des paraboles, cela s'explique car l'équation de droite contient toujours x²

ben alors ce ne sont pas des "équations de droites"
allez, j'arrête de t'embêter
f(x)=x²
g(x)=(x-5)²=f(x-5)
ou encore
g(x+5)=f(x)
si M(x,y) est point du graphe de f, alors M'(x+5,y) est point du graphe de g
on obtient M' à partir de M par une translation de vecteur de coordonnées (5,0)
h(x)=(x+2)²-3 = f(x+2)-3
ou encore
h(x-2)=f(x)-3
si M(x,y) est point du graphe de f, alors M'(x-2,y-3) est point du graphe de h
on obtient M' à partir de M par une translation de vecteur de coordonnées (-2,-3)
C'était g(x) = x² - 10x + 25 autant pour moi
sinon merci beaucoup !! , mais comment faire pour m(x) et l(x) car les paraboles sont plus "fines" que f(x) on ne peux pas dire que c'est une translation ou une simétrie
je te fais la transformation de en
d'abord mettre la fonction sous forme canonique
on va, pour clarifier la situation, passer par une courbe intermédiaire
soit M(x,y) un point du graphe de f, alors
alors le point de coordonnées
tu montreras que et inversement
on passe de à
par une translation de vecteur
de coordonnées
soit alors M' de cordonnées
tu montreras que et inversement
on passe de à
par une dilatation orthogonale d'axe x'Ox et de rapport -2
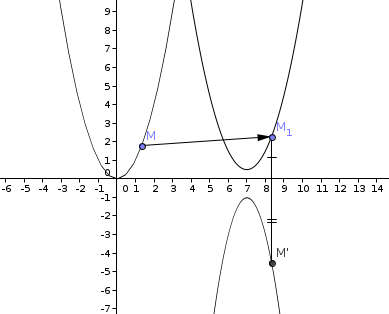
il n'y a pas qu'une seule solution à l'exercice
Soit O l'origine du repère, c'est aussi le sommet de la parabole
Soit S le sommet de
Soit G barycentre du système (O,1), (S,2)
Ses coordonnées sont donc
alors est l'image de
par l'homothétie de centre G, de rapport -1/2
En effet, soit M de coordonnées (x,y) un point de , donc y=x²
son image M' de coordonnées (x',y') par cette homothétie est donnée par les équations :
et tu vérifieras que x' et y' sont liés par la relation y'=-2x'²+28x'-99
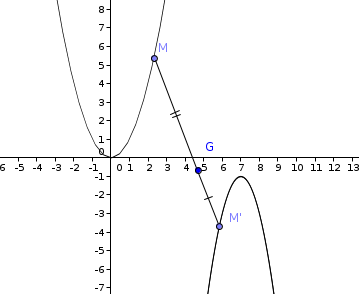
Un gros gros merci !
mais je ne comprends pas trop cette partie :
passer de m(x) à m1(x), où passe le -2
et
comment prouver que M1 appartient à la courbe Gm1 
où passe le -2
il est passé dans la dilatation qui succède à la translation
j'ai décomposé la transformation en deux étapes
et pour vérifier : il faut montrer que les coordonnées du point translaté vérifient l'équation de la courbe.
N'étant qu'un seconde, je n'ai jamais vu le voc souligné et en gras donc je ne sais pas si j'ai le droit de l'utiliser
on passe de M1 à M' par une dilatation orthogonale d'axe x'Ox et de rapport -2
Soit G barycentre du système (O,1), (S,2)
alors Cm est l'image de Cf par l'homothétie de centre G, de rapport -1/2
bah, ça dépend des pays
ton prof te demande-t-il réellement par quelle transformation on peut passer de à
?
si oui, tu me listeras les transformations que tu as vues en cours, qu'on puisse éventuellement trouver quelque chose qui colle à ton programme.
la question exacte est : Comment obtient on les courbes associés de k,l et m à partir de la courbe de f
et donc je suis en seconde, en france, et j'ai vu les transformations de vecteurs et symétrie, c'est tout
en sachant qu'on à ce dm sur les fonctions trinômes sans en avoir encore parlé en cours ..
les transformations de vecteurs
les translations, tu veux dire ?
et bien avec les translations et symétries (droites ou centrales), on ne peut transformer en
les translations et symétries (droites ou centrales) génèrent ce qu'on appelle les isométries
celles-ci conservent les distances.
le facteur -2 de x² pour modifie ces distances.
dis-moi comment le prof présentera son corrigé.

 svp
svp