Bonjour.

Appelons A et B les points d'affixes a et b. dire que |a| = |b| = 1 signifie que A et B sont sur le cercle de centre O et de rayon 1. Par ailleurs, le point S d'affixe a+b est le point tel que (OASB) est un parallélogramme (et même un losange). Je te laisse faire les dessin.

A plus RR.

oui mais c'est comme ça qu'on calcule module de a-b?? je ne vois pas où vous voulez en venir...

a = x + iy
|a| = 1
|a|² = 1
x² + y² = 1

b = z + ip
|b| = 1
|b|² = 1
z² + p² = 1

a+b = x+z + i(y+p)
|a+b|² = (x+z)² + (y+p)²

(x+z)² + (y+p)² = (V3)²
(x+z)² + (y+p)² = 3

x²+z²+2xz + y²+p²+2yp = 3
x²+y²+2xz + z²+p²+2yp = 3
1 + 2xz + 1 + 2yp = 3
2xz + 2yp = 1
xz + yp = 1/2

a-b = (x-z) + i(y-p)
|a-b|² = (x-z)² + (y-p)²
|a-b|² = x²+z²-2xy + y²+p²-2yp
|a-b|² = x²+y²-2xy + z²+p²-2yp
|a-b|² = 1-2xy + 1-2yp
|a-b|² = 2-2(xy + yp)
|a-b|² = 2 - 2*(1/2) = 1
|a-b| = 1

Vérifie.  

ha merci cette solution je l'ai déjà tenté...je trouve bien la même chose mais n'auriez vous pas une autre solution qui ne fait pas utiliser a = x+iy ou b=z+ip??

Mais sinon dans ce cas comment on peut trouver un exemple de coupe vérifiant cette condition?

Reprends mon dessin : Le triangle OAB est équilatéral et donc, AB = |b-a| = 1.

A plus RR.

Comme raymond:

Appelons A et B les points d'affixes a et b. dire que |a| = |b| = 1 signifie que A et B sont sur le cercle de centre O et de rayon 1.

On place des points A et B sur ce cercle (même si ils ne sont pas situés adéquatement, cela n'a pas d'importance pour le raisonnement qui suit.)



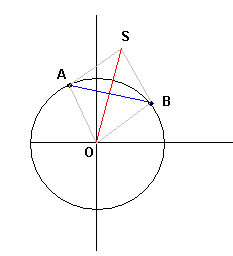
On place le point S tel que vecteur(OS) = vecteur(OA) + vecteur(OB)

S est donc à l'affixe a+b

On doit donc avoir |OS| = V3

vect(OB) = vect(AS) et OB = OA = 1 ---> le quadrilatère OASB est un losange.

Al kashi dans le triangle OAS :
OS² = OA² + AS² - 2.OA.AS.cos(OAS)
3 = 1 + 1 - 2*1*1.cos(OAS)
cos(oAS) = -1/2
angle OAS = 2Pi/3

et comme OASB est un losange, angle OAB = (1/2).angle OAS = Pi/3
OA = OB --> triangle OAB isocèle en O --> angle ABO = angle OAB = Pi/3

Le triangle OAB a ses 3 angles égaux à Pi/3 --> il est équilatéral.
Et donc AB = OA = 1

AB = 1 --> |a-b| = 1
-----
Sauf distraction.