Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

complexe

Posté par
meriemm 29-09-10 à 20:05

z1 et z2 sont deux nombres complexes de module 1. On notera α (alpha) un argument de z1 et β un argument de z2.

1°) a) Démontrer que (z1 + z2)² / (z1*z2) est un réel positif ou nul.

b) Dans quel cas est-il nul ?

2°) Le plan orienté est rapporté au repère orthonormal direct ( O ; vecteur(u) ; vecteur(v) ). Soient A et B deux points d'affixes respectives a et b. On suppose que A, O et B ne sont pas alignés. Calculer en fonction de a et b l'affixe Z du barycentre I du système {(A, |b|), (B, |a|)}.

3°) a) Montrer que Z²/ab est réel strictement positif.

b) Exprimer arg Z en fonction de arg a et de arg b.
  

je  bloque a la 3e question

Posté par
cailloux Correcteurre : complexe 29-09-10 à 23:41

Bonsoir,

Tu dois pouvoir montrer que:

3$Z=\frac{|ab|}{(|a|+|b|)^2}\,\frac{\left(\frac{a}{|a|}+\frac{b}{|b|}\right)^2}{\frac{a}{|a|}\,\frac{b}{|b|}}

et te servir de la question 1) en posant Z_1=\frac{a}{|a|} et Z_2=\frac{b}{|b|} tous deux de module 1

Posté par
cailloux Correcteurre : complexe 29-09-10 à 23:43

Plutôt:

3$\frac{Z^2}{ab}=\frac{|ab|}{(|a|+|b|)^2}\,\frac{\left(\frac{a}{|a|}+\frac{b}{|b|}\right)^2}{\frac{a}{|a|}\,\frac{b}{|b|}}

Posté par
meriemmre : complexe 30-09-10 à 21:10

merci aprés avoir fait cela je dois developper le carré ?

Posté par
cailloux Correcteurre : complexe 30-09-10 à 21:29

Mais pas du tout!

On suppose que a et b sont non nuls sinon A et O ou B et O seraient confondus.

3$\frac{Z^2}{ab}=\frac{|ab|}{(|a|+|b|)^2}\,\frac{\left(\frac{a}{|a|}+\frac{b}{|b|}\right)^2}{\frac{a}{|a|}\,\frac{b}{|b|}}

D' après la question 1):

3$\frac{\left(\frac{a}{|a|}+\frac{b}{|b|}\right)^2}{\frac{a}{|a|}\,\frac{b}{|b|}}

qui est de la forme \frac{(Z_1+Z_2)^2}{Z_1Z_2} avec |Z_1|=|Z_2|=1

est un réel positif!

De plus, il ne s' annulle jamais car a et b sont non nuls et b\not=-a car il est spécifié que O,A et B sont non alignés.

Donc 3$\frac{\left(\frac{a}{|a|}+\frac{b}{|b|}\right)^2}{\frac{a}{|a|}\,\frac{b}{|b|}} est un réel strictement positif.

Et 3$\frac{|ab|}{(|a|+|b|)^2} est aussi un réel strictement posititif (toujours parce que a et b non nuls).

Donc \frac{Z^2}{ab} est un réel strictement positif.

Posté par
cailloux Correcteurre : complexe 30-09-10 à 21:51

Pour la suite des événements:

On tombe sur Arg(Z)=\frac{Arg(a)+Arg(b)}{2}\;\;[\pi]

Le modulo \pi est très génant; après tout, les points A et B étant donnés, le point M d' affixe Z est parfaitement défini et unique.

Des considérations géométriques (M\in [AB]) permettent de lever cette "indétermination":

Arg(Z)=\frac{Arg(a)+Arg(b)}{2}\;\;[2\pi]

Un dessin pour l' interprétation géométrique:

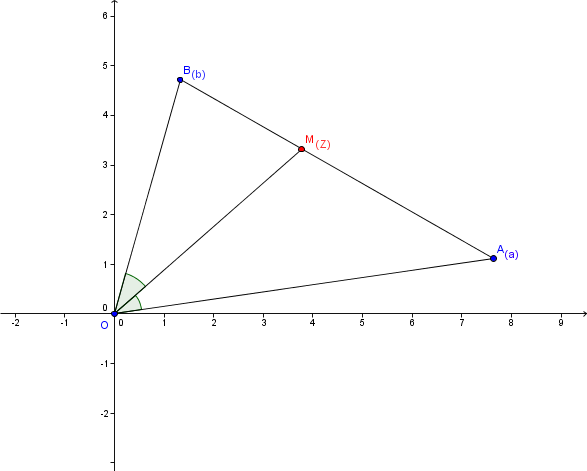
complexe

Le point M(Z) est le pied de la bissectrice issue de O du triangle OAB

Posté par
cailloux Correcteurre : complexe 30-09-10 à 21:57

Un petit rectificatif à 21h29:

De plus, il ne s' annulle jamais car a et b sont non nuls et b\not= ka avec k\in\mathbb{R}^{-*} car il est spécifié que A,B et O sont non alignés.

Posté par
meriemmre : complexe 30-09-10 à 22:36

mercii beaucoup je viens de comprendre !!!

Posté par
cailloux Correcteurre : complexe 30-09-10 à 22:42

De rien meriemm


Rechercher
Menu
Espace membre
8 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !