Inscription / Connexion Nouveau Sujet
Voici ce que tu aurais dû écrire :
=( (zzbarre -2zbarre) /(z barre -2) - ( zzbarre -2z)/( z barre -2)) / (z-2)
J'ai trouvé que ce calcul était égal à 2z -2zbarre / zzbarre -2z -2zbarre +4
Le nominateur et le dénominateur sont imaginaires. Cette expression est donc imaginaire pur
Reprends plutôt ma réponse de 22h37.
2 est un réel
est un réel (voir question 3a)
est un imaginaire pur car...
Donc est un imaginaire pur.
Réfléchis un peu 
Si zbarre=z, alors z est un nombre réel...
La question 2 traitait de l'ensemble des points invariants qui est l'axe réel.
Or justement dans cette question, les points M ne sont pas sur l'axe des réels....
Donc si une des droites se situe sur l'axe des réels et l'autres sur l'axe des imaginaires alors les droites sont perpendiculaires
Prends la peine de relire ce qui a été écrit à la page précédente à partir du message "30-12-16 à 15:21"
Voici un résumé des messages importants ;
"Pour la question 4, il faut généraliser la question 1c).
Donc tu démontres que si M un point quelconque non situé sur la droite AB, alors les droites (AM) et (MM') sont perpendiculaires."
"Il faut donc démontrer que .
Pour cela il faut calculer .
Cela revient donc à calculer et montrer que c'est égal à
"
"Commence par transformer l'expression et démontre que le résultat est un imaginaire pur."
Maintenant que tu as démontré que l'expression est un imaginaire pur, tu relis les lignes précédentes à l'envers (à partir de la dernière)
Oui bien sur ça c'est la leçon du coup nous pouvons dire que cet argument est le même que celui de zm'-zm/zm-za
Donc l'angle Am mm' est de pi/2, soit 45 degrés
Les droites (am) et (mm') sont donc perpendiculaires
Cette rédaction convient-elle ?
" l'angle Am mm' est de pi/2, soit 45 degrés "
45 degrés ??? 
De plus l'angle (AM,MM') n'est pas nécessairement égal à pi/2.
En fait, .
Donc si M est un point quelconque non situé sur la droite (AB), alors les droites (AM) et (MM') sont perpendiculaires
Voici la question 4 :
"4) Soit M un point quelconque non situé sur la droite AB. Généraliser le résultat de la question 1c"
Nous avons bien généralisé le résultat de la question 1c) et nous l'avons démontré.
Que veux-tu de plus ?
"5) Soit M un point distinct de A. Déduire des questions précédentes une construction du point M' image du M par f."
Il faut envisager deux cas.
1er cas : M est sur l'axe des réels.
2ème cas : M n'est pas sur l'axe des réels.
Pour la question 5, je dirai que m' est le symétrique de m par symétrie axiale
Étant donné que m se situe sur l'axe des imaginaires, m' l'est aussi par symétrie, non ?
m se situe sur l'axe des imaginaires,
Où est-ce écrit dans l'énoncé ?
On dit seulement que M un point distinct de A. Donc M peut se situer partout dans le plan complexe sauf sur le point A.
m' est le symétrique de m par symétrie axiale
Non... Quelle symétrie ?
L'énoncé dit ceci :
Déduire des questions précédentes une construction du point M' image de M par f.
Il faut donc que tu donnes toutes les instructions pas à pas pour pouvoir construire le point M'
Comme je l'ai déja écrit :
Il faut envisager deux cas.
1er cas : M est sur l'axe des réels.
2ème cas : M n'est pas sur l'axe des réels.

En fait, je te propose ceci :
Tu prends une feuille de papier.
Tu représentes les points A et B.
1er cas :
Tu choisis un point M distinct de A sur l'axe réel et tu construis sont image M' (évident...)
2ème cas :
Tu choisis un point M distinct de A non situé sur l'axe réel, n'importe où dans le plan et tu construis son image M'.
Pour ce faire, tu vas passer par quelques étapes qu'il faudra décrire.
C'est ce qu'on appelle la construction de M'.
Pour cette construction, tu vas devoir utiliser les résultats des questions 3c et 4.
Commençons par le 1er cas :
Tu choisis un point M distinct de A n'importe où sur l'axe réel et tu construis sont image M'.
La position de M' est évidente, non ?
Voici un petit cadeau de Nouvel-An... Je vais résoudre cette question 5. 
Il faut envisager deux cas.
1er cas : M est sur l'axe des réels.
Puisque l'ensemble des points invariants par f est l'axe des abscisses, nous en déduisons que M' = M.
Donc pas de construction, puisque M' = M.
2ème cas : M n'est pas sur l'axe des réels.
Nous plaçons un point M distinct de A non situé sur l'axe réel, n'importe où dans le plan complexe.
La construction du point M' sera écrite en rouge.
Selon la question 3c), nous savons que les droites (AM) et (BM') sont parallèles.
Traçons donc la droite (AM) et, par le point B, traçons une droite (d1) parallèle à (AM).
Par la question 3c), nous savons que le point M' appartient à (d1).
Par la question 4, nous savons que les droites (AM) et (MM') sont perpendiculaires.
Par le point M, traçons une droite (d2) perpendiculaire à la droite (AM).
Par la question 4, nous savons que le point M' appartient à (d2).
Puisque le point M' appartient à (d1) et à (d2), nous en déduisons que le point M' est le point d'intersection entre (d1) et (d2).
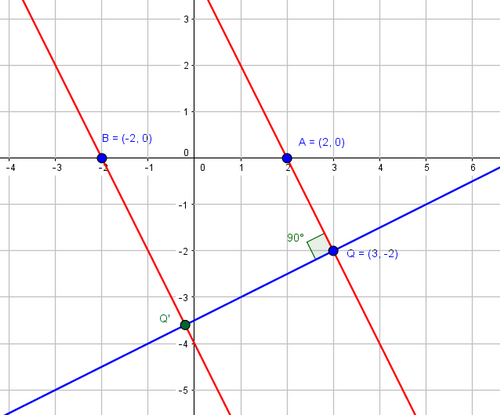
Voici la figure demandée dans cette question 4 où le point M est le point Q d'affixe 3-2i