Inscription / Connexion Nouveau Sujet
convergence série de Fourier
Bonjour,
j'ai quelques confusion entre les différentes convergences pour les séries de Fourier
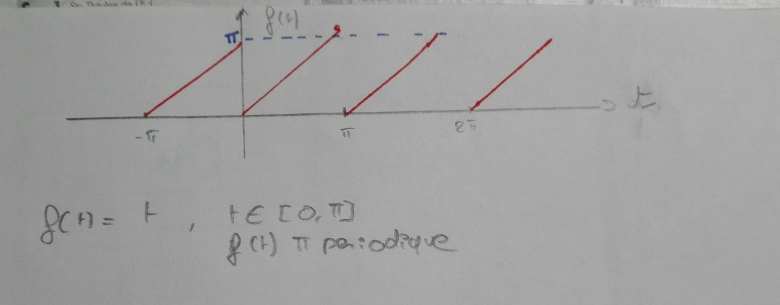
On a f(x) = t  périodique pour t
périodique pour t  [ 0 ;
[ 0 ;  [
[
J'ai écrit formellement la série
Voici ce que j'ai commencé à faire, mais c'est assez confus
On doit maintenant dire si il y a
• Convergence ponctuelle (ou simple)
Je ne vois pas comment faire avec le sinus ..
• Convergence absolue
Pas de convergence asolue car 1/n diverge (comparaison au série de Riemman)
• Convergence en norme quadratique
Convergence en norme quadratique car 1/n² converge (Rieman)
Merci d'avance pour votre aide 
Bonjour
Tu dois dire si pour tout t réel, la série évaluée en t converge vers f(t) (d'ailleurs tu as fait une confusion avec les x et les t)
Merci pour votre réponse,
Montrer que la série converge vers f(t) est la dernière question de l'exercice (si la série Sn converge et f(t) continue (par morceaux) alors Sn converge vers f)
Mais c'est l'étude de la convergence de la série, et les 3 "types" de convergence qui ne sont pas claires pour moi
Merci d'avance 
Je t'expliquais justement ce qu'étais la convergence ponctuelle (ou simple)
ça veut dire qu'en tout point, la série évaluée en ce point converge vers l'image de ce point
C'est la convergence la plus simple au sens de l'intuition, mais ce n'est pas la plus puissante en terme mathématique
Bonsoir !
Il y a des résultats de ton cours (probablement théorème de Dirichlet) qui permettent de répondre à la première question.
La raison que tu donnes pour la convergence absolue n'est pas correcte : il faut étudier la série , il n'y a pas d'équivalent en
Merci pour votre réponse, 
• Pour la convergence ponctuelle/simple
dans le cours, on a écrit que si une fonction périodique a une limite à droite et à gauche en a,notées f(a-) et f(a+) , la série converge vers
On aurait donc ici la convergence ponctuelle vers , c'est ca ?
• Pour la convergence absolue, je ne vois pas vraiment comment étudier la série
Je l'avais majorée par 1/n mais cela n'apporte rien car 1/n diverge ..
Etudier les variation avec la dérivée serait une possibilité ?
Merci encore 
Ton calcul donnant n'est valable que pour des valeurs de
que tu ne précises pas.
Tu devrais donner un résultat qui dépend de .
Pour la convergence absolue, le plus simple à mon avis c'est d'écrire :
et conclure, à condition de savoir que la série
est convergente.
Bonsoir,
on souhaite déterminer la convergence absolue de
J'ai essayé
- la règle des séries alternées (inapplicable car le sinus varie entre -1 et 1)
-en majorant/minorant la valeur absolue on a du 1/n qui diverge donc inexploitable
Je ne vois pas vraiment comment m'en sortir
avez vous des pistes ?
merci d'avance
bonne soirée 
*** message déplacé ***
Merci pour votre réponse
• Pour la convergence simple,
j'étais parti du graphe ci joint, et pour n'importe quel a (lieu avec une limite à gauche et à droite) j'avais  /2
/2
C'est donc faux ?
• Pour la convergence absolue
on peut affirmer que la série cos(4nt)/2n converge comme le coefficient 1/2n converge non ?
Merci d'avance 
Hello! Comme |sin(2nx)| ne converge pas vers 0, il existe e>0 et une sous suite Up tel que
pour tout p
*** message déplacé ***
• Pour la convergence absolue
on peut affirmer que la série cos(4nt)/2n converge comme le coefficient 1/2n converge non?
Ça veut dire quoi le coefficient converge ?
Bonjour
Je pensais au coefficient de la série trigonométrique , le -1/2n qu'il y a devant le cosinus tend vers 0 quand n grand
Je t'ai mis en place la minoration d'une série de réels positifs par une somme de séries, l'une divergente, l'autre convergente.
Si tu n'arrives pas à conclure sans faire du surréalisme, je ne vois pas quoi dire de plus !
Attention ! Tu fais du multi-post.
Je t'ai déjà donné la réponse dans ![]() convergence série de Fourier
convergence série de Fourier
*** message déplacé ***
Bonjour,
tout d'abord désolé pour le multi post, je pensais que comme mon problème n'était plus sur la convergence des séries de fourrier en général mais sur la convergence absolue d'une série trigo il fallait en faire un sujet séparé :/
luzak désolé de ne pas avoir compris vos explication on débute les séries et les raisonnements et automatismes sont encore compliqués
Cela fait partie des débuts !
Si et
divergente, alors
est divergente.
Si sont convergentes alors
est convergente.
Si tu ne connais pas ces résultats, attends d'avancer dans l'étude des séries.
................................
Je sais qu'il y a des profs au comportement curieux mais faire étudier les séries de Fourier et savoir (ton intervention laisse entendre que c'est connu) que est convergente me laisse une impression de 4ème dimension.
et savoir (ton intervention laisse entendre que c'est connu) que
C'est vrai que c'est surprenant car c'est pas la série la plus simple à étudier . De manière assez élémentaire , une transformation d'Abel permet de conclure il me semble mais c'est quand même un outil avancé ...
Bonsoir
merci beaucoup
je crois que je viens de comprendre la méthode de minoration par une série divergente
On a donc la série sin(nt)/n
-qui converge ponctuellement vers  /2
/2
- qui ne converge pas absolument
- qui converge en norme quadratique
Zrun dans notre cours nous avons dit "qu'un résultat du à Abel est que la série des an cos(nx) + bn sin(nx) converge si an et bn décroissants et tendent vers 0" mais nous n'avons pas le théorème qui permet de le prouver
Bonne soirée 
Je te répète que la série ne converge pas ponctuellement vers .
Cette somme n'est correcte que pour des valeurs particulières de .
Reprends ton dessin, tu vois bien qu'en un point de continuité la demi-somme des limites à droite, à gauche n'est pas : pour
la fonction est continue en
et la demi-somme des limites est égale à
, pas toujours ce que tu indiques.
Bonjour,
pour la convergence ponctuelle, on aurait donc
- pour les points de continuité, la série converge, donc elle converge vers la fonction f(t) = t
- Pour les points de "non continuité" (t = n ) on a convergence vers
) on a convergence vers  /2
/2
C'est bien ça ?
En tous cas merci pour votre aide je commence à y voir plus clair petit à petit 
bon dimanche
Pas tout à fait : la limite est lorsque
.
Pour les autres intervalles il faut corriger (tu peux utiliser ton dessin) : .


 ) :
) :

