Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques

1 2 +

Niveau Licence Maths 1e ann
Partager :

Convergence simple et uniforme

Posté par
mimibeg 28-02-11 à 16:59

Bonjour,

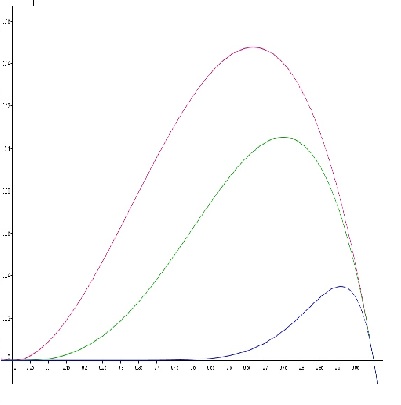
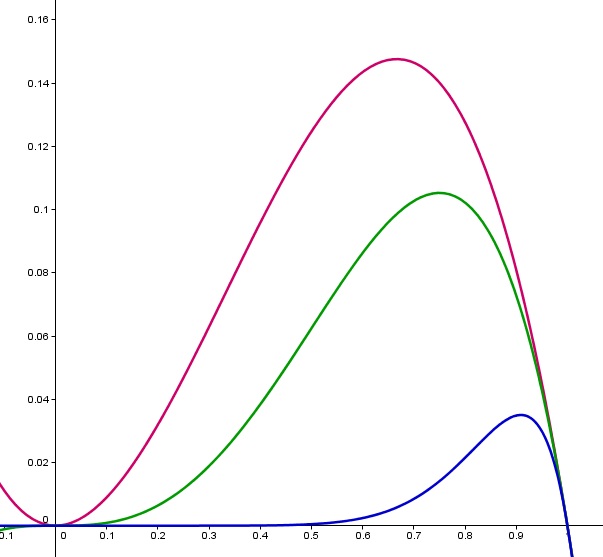
J'ai un problème depuis quelques jours avec un exercice de math, je dois étudier la convergence simple de la suite de fonction définie sur [0,1] par fn(x)=sin(xn(1-x)) puis ensuite étudier sa convergence uniforme.
J'ai du mal à trouver la fonction vers la quelle fn converge simplement pourriez vous m'aider?

Merci d'avance

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:04

Bonjour,

x étant fixé entre 0 et 1, vers quoi converge x^n ?

Posté par
mimibegRE 28-02-11 à 17:05

vers 0 si x =0 ou vers 1 pour le reste

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:08

Ah non, c'est faux: si x=\fr 12 par exemple, x^n converge-t-il vers 1?

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:12

Ah oui j'ai inversé 1 si x=1 et 0 sinon

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:14

Ah oui donc faut séparer les deux cas et on a forcément fn tend vers f(x)=0 c'est ça?

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:14

Ok, donc vers quoi tend x^n(1-x) ?

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:18

Maintenant que j'ai la convergence simple vers 0 est ce que lim sup(fn(x)) = 0 parce que je me fais à chaque fois avoir la dessus

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:20

SA limite supérieure ou la convergence uniforme?

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:21

Il me semble que si fn converge uniformement alors la limite suppérieure de fn-f est égale à 0 c'est pas ça?

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:25

Tu confonds avec la limite lorsque n tend vers l'infini de la borne supérieure de |f_n-f|.

Attention! La notion de limite supérieure existe aussi en Analyse, mais c'est autre chose.

Donc pour répondre à ta question, non, la convergence simple n'entraîne pas forcément la convergence uniforme.

Ici f = 0, donc tu es ramenée à chercher, à n fixé, le sup de |f_n(x)| pour x variant entre 0 et 1.

En observant que cette fonction est positive, tu peux par exemple étudier ses variations sur [0;1] (je te rappelle qu'on a fixé n)

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:26

Citation :
En observant que cette fonction est positive


-> Je parlais de f_n

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:37

On a fixé n? mais il faut quand même étudier plusieurs fonctions alors (f1(x); f2(x) ...) ?

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:38

C'est pour ça qu'on le fait d'un seul coup d'un seul en prenant n quelconque!

Posté par
mimibegre : Convergence simple et uniforme 28-02-11 à 17:43

ok donc je dois étudier la dérivée pour avoir les variations je vais essayer merci

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 28-02-11 à 17:47

Oui voilà et quand tu auras le maximum, qui dépend de n, montre qu'il tend vers 0 quand n tend vers l(infini puis conclus!

Je dois y aller, bon courage!

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 10:08

Tu t'en sors?

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 11:22

A vrai dire moyennement j'ai trouvé que la dérivée en valeur absolue était inférieure à n*xn-1 pour x € [0,1[ mais je ne vois pas le rapport avec la convergence uniforme

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 11:45

J'ai du me tromper quelque part parce que la ça voudrait dire qu'on a une fonction constante ...

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 11:47

Reprenons: pour commencer,x^n(1-x) prend ses valeurs dans [0;1], et le sinus est croissant sur cet intervalle.

Donc les variations de f_n à n fixé sont les mêmes que celles de x^n(1-x).

Quelles sont les variations de cette fonction sur [0;1], et où atteint-elle son maximum ?

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 11:51

Ah ok j'avais essayé avec la dérivée mais impossible de calculer son signe ...
Pour xn(1-x) j'ai une dérivée négative donc c'est décroissant donc le maximum est atteint en 0 et c'est 0?

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 11:56

La dérivée n'est pas tout le temps négative! Qu'as-tu comme dérivée?

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 12:00

Ah non excuse moi je me suis trompée d'expression sin(xn(1-x)) est croissante sur [0,n/(n-1)] et décroissante après

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 12:02

Presque! Il faut remplacer ton n-1 par n+1, ok?

Donc que vaut le maximum de f_n sur [0;1], à n fixé ?

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 12:04

J'ai n+1sur ma feuille et j'écris n-1 ...
ça vaut sin((n/(n+1))n*(1-n/(n+1))) et ça devrait tendre vers 0

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 12:09

Oui mais il faut bien le justifier!

Enlève pour l'instant ton sinus et transforme le premier facteur afin de lever l'indétermination, le second tendant clairement vers 0.

Posté par
mimibegre : Convergence simple et uniforme 01-03-11 à 12:12

ok je vais faire ça en tout cas merci beaucoup !

Posté par
Tigweg Correcteurre : Convergence simple et uniforme 01-03-11 à 12:13

Je t'en prie!

Posté par
mimibegre : Convergence simple et uniforme 02-03-11 à 13:54

Excusez moi de vous rederanger mais je voulais savoir: quand on sait qu'une suite de fonction converge simplement et uniformement est ce que ça nous donne quelque chose sur la suite des dérivées?

Posté par
Camélia Correcteurre : Convergence simple et uniforme 02-03-11 à 15:03

Bonjour

NON la suite des dérivées fait n'importe quoi! En revanche si la suite des dérivées converge uniformément et la suite de fonctions converge en au moint un point, la suite des fonctions converge vers une fonction dérivable, dont la dérivée est bien la limite de la suite des dérivées.

Posté par
mimibegre : Convergence simple et uniforme 02-03-11 à 15:15

D'accord donc si après l'étude d'une suite de fonctions on me demande d'étudier la convergence de la suite des dérivées, je dois refaire toute l'étude?

Posté par
Camélia Correcteurre : Convergence simple et uniforme 02-03-11 à 15:17

Oui, il faut le faire!

Posté par
Leonegresre : Convergence simple et uniforme 03-09-12 à 22:13

Bonjour Camélia, et bonjour Tigweg ,

Je me permets de relancer ce topic, car débutant dans ce domaine, j'aimerais aborder avec vous cette étude de convergence.

J'ai cru comprendre qu'il fallait étudier les variations de :

u'(x) avec u(x)=fn(x)-f(x)

f étant la fonction (nulle) limite simple.

Suis-je sur le bon chemin svp ?

Merci

Posté par
Camélia Correcteurre : Convergence simple et uniforme 04-09-12 à 14:46

Oui, tu cherches les variations de u_n(x) pour avoir le sup, et pour ce faire tu regardes le signe de la dérivée.

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 15:12

On a donc :

u(x)=f_n(x)-f(x)=f_n(x)-0=sin(x^n(1-x))

On a :

u'(x)=[nx^{n-1}(1-x)-x^n]cos(x^n(1-x))= 0 sur [0,1] pour sauf erreur :

x=0
x=1
x=\frac{n}{n+1}

C'est ça jusque là ?

Convergence simple et uniforme

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 15:15

Comme ça, c'est plus joli.

Convergence simple et uniforme

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 17:31

Je ne sais pas si ce que j'ai mis dans mon message Posté le 04-09-12 à 15:12 est juste, mais si tel est le cas, j'avoue avoir bien du mal (sans regarder la courbe) à définir là où u'(x)>0 et là où u'(x)<0

Un petit peu d'aide serait la bienvenue.

Merci

Posté par
GaBuZoMeure : Convergence simple et uniforme 04-09-12 à 17:41

Même avec u'(x)=x^{n-1}(n-(n+1)x)\,\cos(x^n(1-x)) ?

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 17:46

Et bien écoute, je t'avoue que je suis en train de regarder et vraiment, ça ne me saute pas aux yeux ...

Posté par
GaBuZoMeure : Convergence simple et uniforme 04-09-12 à 17:49

Du mal à trouver le signe d'un produit de 3 facteurs ?
Pour le dernier, n'oublie pas que x\in[0,1].

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 17:57

Citation :
Du mal à trouver le signe d'un produit de 3 facteurs ?


Et oui, ça arrive ... et même pire.

cos(x^n(1-x))\geq 0

pour le reste je ne vois pas.ou pas encore

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 18:03

x^{n-1}\geq 0


ça progresse .....

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 18:12

ça y est, ok, c'est bon.

En prenant par exemple x=\frac{n}{n+2}<\frac{n}{n+1}, on a u'(x)>0

donc croissante, puis décroissante.

Donc si j'ai bien compris, j'ai :

sup_{x\in [0,1]}\mid f_n(x)-f(x)\mid=\mid\frac{n}{n+1}\mid

C'est bien cela ?

Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 18:15

Ouh là ... je me demande si je ne dis pas des grosses c.....

Posté par
GaBuZoMeure : Convergence simple et uniforme 04-09-12 à 18:17

Oui, des vraiment grosses !

Posté par
carpediemre : Convergence simple et uniforme 04-09-12 à 20:58

salut

sur l'intervalle [0,1] la fonction sinus est croissante (strictement) donc (par composée) f a même variation que le polynome x --> xn(x-1) dont l'étude est élémentaire ....

ainsi ln (u) et exp(u) ont même variation que u ....


ça allège l'écriture et évite des calculs non nécessaires ....


Posté par
Leonegresre : Convergence simple et uniforme 04-09-12 à 23:29

Je n'ai rien compris ...

Remarquez, dans ma vie professionnelle, il y a plein de choses "élémentaires" que je pourrais présenter et qui échapperaient  au premier venu.

C'est d'ailleurs pour cela que quand j'explique à des tiers quelque chose qui relève de mes compétences (reconnues), je me contente de les accompagner et non pas de leur dire que "c'est comme ci" ou "comme ça".

Pour l'instant, je cherche juste à comprendre.

Peut-être qu'après, je chercherais à savoir ...

Posté par
Leonegresre : Convergence simple et uniforme 05-09-12 à 08:36

Avec les interventions (parfois désagréables de certain(s) et pas forcément très constructives ...) j'en arrive à ne plus rien comprendre ...

Donc afin d'y voir plus clair (et tant pis pour l'éventuelle redondance ...)  :

Est-ce que ce que j'ai mis dans mon message Posté le 04-09-12 à 15:12 est juste à propos du calcul de u'(x) ?

Est-ce que cela, c'est bon :  cos(x^n(1-x))\geq 0  ?

Est-ce que cela est bon aussi :  x^{n-1}\geq 0  ?

J'en arrive à u'(x)=0 pour x=\frac{n}{n+1} , est-ce correct ?

Ma fonction u(x)=f_n(x)-f(x) où f(x)=0 est-elle bien croissante de 0 à f_(\frac{n}{n+1}), puis décroissante vers 0  ?


J'ai Sup_{[0,1]}\mid f_n(x) \mid=f_n(\frac{n}{n+1})=sin((\frac{n}{n+1})^n(1-\frac{n}{n+1})) \rightarrow 0 quand n \rightarrow +\infty

Est-ce bon ?

Si tel n'est pas le cas, où est-ce que ça cloche s'il vous plaît ?

Merci

Posté par
carpediemre : Convergence simple et uniforme 05-09-12 à 10:23

il y a un théorème relativement élémentaire puisque autrefois !! vu au lycée qui donne les variations de la composée f o g de deux fonctions connaissant les variations de f et g ...

en particulier si f est (strictement) croissante alors g et f o g ont même variation ...

ce qui évite d'avoir à dériver une composée et à étudier le signe d'une expression compliquée ...

Posté par
carpediemre : Convergence simple et uniforme 05-09-12 à 10:25

petite remarque ::

la nullité de la dérivée ne permet pas de conclure quant à son signe ...

en d'autre terme la résolution de l'équation f'(x) = 0 ne permet pas (en général) de connaitre le signe de f' ....

1 2 +


Rechercher
Menu
Espace membre
25 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1724 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !