Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Courbe

Posté par
fenerisikiyim 28-01-23 à 19:51

Bonsoir,
J'ai un exercice où il faut montrer que f(x)=g(x)
avec f(x)=((1+cos(x))/(2-cos(x)))
et g(x)= -1+sqrt(3) (((2-sqrt(3))/(ℯ^(ί x)-2+sqrt(3)))-((2+sqrt(3))/(ℯ^(ί x)-2-sqrt(3))))
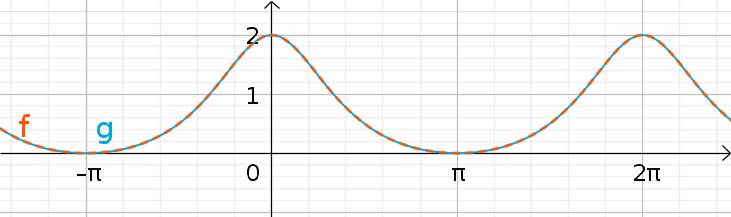
ça je l'ai fais ce n'est pas un probleme mais lorsque je  met les 2 expressions sur geogebra (par exemple) je n'ai pas la meme courbe et pourtant  f=g y a une égalité
Ma question est la suivante pourquoi je n'ai pas la meme courbe ?
ma question est peut-etre bete mais je me posais la question ^^
Bonne soirée à vous

Posté par
GBZMre : Courbe 28-01-23 à 21:15

Bonsoir,
C'est bien ça que tu voulais écrire ?

\large g(x)= -1+\sqrt{3} \left(\dfrac{2-\sqrt{3}}{e^{i x}-2+\sqrt{3}}-\dfrac{2+\sqrt{3}}{e^{i x}-2-\sqrt{3}}\right)

Le code à insérer entre balises LTX :
\large g(x)= -1+\sqrt{3} \left(\dfrac{2-\sqrt{3}}{e^{i x}-2+\sqrt{3}}-\dfrac{2+\sqrt{3}}{e^{i x}-2-\sqrt{3}}\right)

Posté par
GBZMre : Courbe 28-01-23 à 21:38

GeoGebra est bien d'accord que les deux fonction sont égales :

Courbe

Posté par
fenerisikiyimre : Courbe 28-01-23 à 21:43

Je ne comprends pas j'ai ecris exactement la meme chose et j'ai des cercles mais pour f(x) je suis d'accord j'ai bien ça.

Posté par
GBZMre : Courbe 28-01-23 à 22:27

As-tu essayé
Re( -1+sqrt(3) (((2-sqrt(3))/(ℯ^(ί x)-2+sqrt(3)))-((2+sqrt(3))/(ℯ^(ί x)-2-sqrt(3)))) )

Posté par
fenerisikiyimre : Courbe 28-01-23 à 22:30

Ah oui d'accord je vois fallait mettre la partie reelle.
Merci à vous bonne soirée

Posté par
fenerisikiyimAnalyse de Fourier 28-01-23 à 22:46

Bonsoir,
J'ai besoins d'aide pour un exercice,
j'ai f(x)=((1+cos(x))/(2-cos(x)))
je devais montrer que :\large f(x)= -1+\sqrt{3} \left(\dfrac{2-\sqrt{3}}{e^{i x}-2+\sqrt{3}}-\dfrac{2+\sqrt{3}}{e^{i x}-2-\sqrt{3}}\right)
c'est fait et maintenant je dois en deduire que \large f(x)=-1+\sqrt{3}+2\sqrt{3} \sum_{n=1}^{inf}(2-\sqrt{3})^{n}cos(nx)
ça ressemble vraiment à la serie de fourier de f
avec a0= -1+\sqrt{3}
an=2\sqrt{3}(2-\sqrt{3})^{n}
mais je ne vois pas comment le montrer
pouvez-vous m'aider svp

*** message déplacé ***

Posté par
lafol Moderateurre : Analyse de Fourier 28-01-23 à 22:59

Bonsoir

chacune de tes fractions est du genre 1 sur 1 moins la raison : ce sont des sommes de séries géométriques ....

*** message déplacé ***

Posté par
elhor_abdelali Correcteurre : Analyse de Fourier 28-01-23 à 23:45

Bonsoir fenerisikitim
Tu peux en effet faire comme le suggère lafol et utiliser le développement bien connu \Large\boxed{\forall z\in\mathbb C~(|z|<1)~,~\frac{1}{1-z}=\sum_{n=1}^{+\infty}z^n}

il suffit pour cela de remarquer que \large\boxed{\dfrac{2-\sqrt{3}}{e^{i x}-2+\sqrt{3}}-\dfrac{2+\sqrt{3}}{e^{i x}-2-\sqrt{3}}=(2-\sqrt3)e^{-ix}\dfrac{1}{1-(2-\sqrt3)e^{-ix}}~+~\dfrac{1}{1-(2-\sqrt3)e^{ix}}}


et donc \large\boxed{f(x)=-1+\sqrt3\left((2-\sqrt3)e^{-ix}\sum_{n=0}^{+\infty}(2-\sqrt3)^ne^{-inx}~+~\sum_{n=0}^{+\infty}(2-\sqrt3)^ne^{inx}\right)}


qui s'écrit aussi \large\boxed{f(x)=-1+\sqrt3\left(\sum_{n=0}^{+\infty}(2-\sqrt3)^{n+1}e^{-i(n+1)x}~+~\sum_{n=0}^{+\infty}(2-\sqrt3)^ne^{inx}\right)}


ou encore \large\boxed{f(x)=-1+\sqrt3\left(\sum_{n=1}^{+\infty}(2-\sqrt3)^ne^{-inx}~+~\sum_{n=0}^{+\infty}(2-\sqrt3)^ne^{inx}\right)} ... sauf erreur de ma part bien entendu

*** message déplacé ***

Posté par
elhor_abdelali Correcteurre : Analyse de Fourier 28-01-23 à 23:48

Pardon c'est plutôt fenerisikiyim

*** message déplacé ***

Posté par
elhor_abdelali Correcteurre : Analyse de Fourier 28-01-23 à 23:57

Ah encore une petite coquille lire plutôt :

... le développement bien connu \Large\boxed{\forall z\in\mathbb C~(|z|<1)~,~\frac{1}{1-z}=\sum_{n={\red0}}^{+\infty}z^n}

*** message déplacé ***

Posté par
fenerisikiyimre : Analyse de Fourier 29-01-23 à 01:34

MAIS OUIIII je n'y avais pas pensé…
Merci à vous 2
Merci Elhor pour le développement t'es un roi

*** message déplacé ***

Posté par
malou Webmasterre : Courbe 29-01-23 à 08:26

attentionextrait de c_faq la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?



toutes les questions d'un même problème doivent être posées dans le même sujet.
merci

Posté par
elhor_abdelali Correcteurre : Courbe 29-01-23 à 12:44

C'est un plaisir fenerisikiyim


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1750 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !