Bonjour,

Comment cela tu ne sais pas comment t'y prendre ? Quelle est la définition d'une fonction périodique, de période ?

Bonjour
clairement  2pi est période de x et  de y. On peut se restreindre ) [0 , 2 Pi]
ou  mieux [-Pi,Pi]
Ensuite x est paire et y impaire  alors on  peut se restreindre à  [0, pi] et compléter la courbe puisque elle est symétrique par rapport à Ox.

@JB2017 : "Clairement" ne constitue pas une preuve, du moins pas dans ce cas précis.

Bonjour,
Une fonction est périodique de période T si f(x+T)=f(x) mais avec cette formule il suffit de remplacer T par la période mais dans ce cas on ne la connait pas, c'est pas comme si on me demandais de montrer que x et y étaient 2pi périodique, la j'aurais pu remplacer T par 2pi

en effet,
cos(x+2pi)=cos(x) et de même pour le sinus donc on retombe bien sur x(t) et y(t)

x paire car x(-t)=x(t) et y impaire car y(-t)=-y(t) donc comment jb2017  a t-il pu conclure qu'on pouvait se retreindre à [0, pi] ?

@ThierryPoma,  ta remarque mon ta faiblesse. "Clairement" est un mot couramment employé en mathématiques. C'est une autre façon de dire que c'est évident, que cela "saute au yeux."  C'est tellement évident qu'il n'y a pas de démonstration à faire.

@JB2017 : Ta dernière remarque montre manifestement que tu ne sais pas lire. Je t'invite à lire en particulier le message du 14-05-17 à 15:23.

La périodicité te permet  de restreindre l'étude sur un intervalle d'amplitude 2pi
c'est à dire  [0, 2pi]  ou bien [-pi,pi].
Pour un explication plus courte je préfère le deuxième choix.
  en effet (x(-t),y(-t))=(x(t),-y(t))=  "le symétrique de (x(t),y(t)) par rapport à Ox"
C'est à dire que  connaissant la partie de la courbe pour t>0 j'en déduis la partie pour t<0 par cette symétrie.
    

Bref je te répond par un silence qui veut dire ce qu'il veut dire!!

ajoute un "s" si tu sait lire.

D'accord, je pense avoir compris, merci !
Et une dernière question : on me demande de faire un DL d'ordre 2 en t=0 de x et y puis d'en déduire l'allure locale de la courbe en t=0
donc pour x(t) je trouve un DL égal à 2-3X^2/2 et pour y(t) un DL égal à 2x
maintenant je conclue comment ? je recherche la tangente y de la courbe ? Puis j'étudie le signe de f(x) - y ?

bonjour

Ou alors je peux étudier les branches infinies ?

Personne ne peut m'aider pour cette dernière question ?

Tu peux remarquer qu'on a pour tout t tel que cos(t) + 1 non nul, y(t) / x(t) = tan(t) : ça donne des repères pour tracer la courbe

pour tes dl, il y a deux problèmes : la variable n'est pas la bonne, et il manque les restes

PS : je ne vois pas trop ce que tu veux dire avec tes "branches infinies" : comment peut-on avoir des branches infinies quand x et y sont bornées n'as-tu pas fait les tableaux de variations de x et de y ?

Bonjour à tous!
Bien que tu ne me donnes pas trop envie de t'aider... Ton développement limité montre clairement dans quels quadrants se situe la courbe au voisinage de (2,0).

Voici la courbe:

Ah oui autant pour moi
Donc x(t)=2-3t^2/2+o(t^2)
et y(t)= 2t+o(t) ?

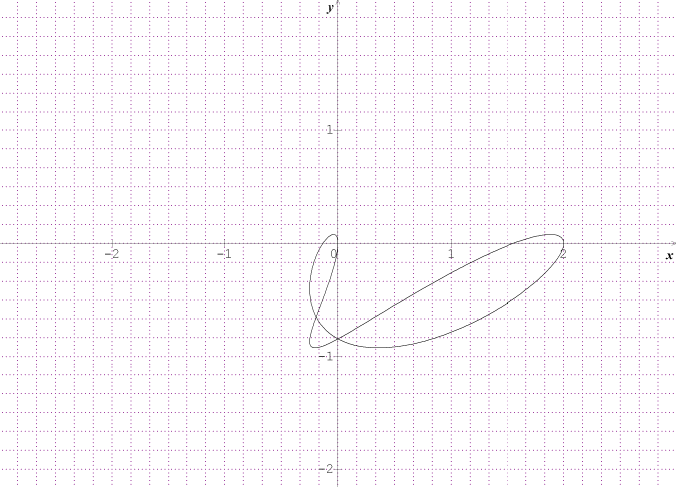
ensuite, quand tu auras réécrit correctement tes dl, tu as dû voir en classe comment t'en servir pour écrire des choses du genre et l'interpréter (les à remplacer par les nombres convenables obtenus dans tes dl)

bonjour Camelia
je me demande si tu ne confonds pas jb2017 et JAGC ?

bonjour Lafol, je n'ai pas besoin d'un deuxième agresseur.
J'ai répondu dans la volonté d'aider et  si ma réponse ne plait pas à  ThierryPoma  qu'il garde sa remarque pour lui et qu'il apporte sa réponse s'il pense qu'il y a un plus à apporter.

Maintenant Lafol, je n'ai pas à éplucher en détails tes messages mais il me semble bien qu'ici et là tu verses assez souvent  dans l'agressivité qui n'est pas toujours constructive.
Maintenant je t'invite à regarder les miens et tu verras que j'ai surement un peu plus que "l'ombre de la moitié du commencement d'une idée de comment on peut le prouver...." et que suis souvent moins agressif que toi.

Si, lafol j'ai bien confondu ! N'empêche, la courbe est jolie!

En fait je ne vois pas du tout comment faire pour étudier l'allure locale de la courbe à partir des DL .. il ne faut pas trouver une tangente ?

bizarre, moi je trouve cette courbe (en rouge pour t entre 0 et pi, en bleu pour t entre -pi et 0, histoire de bien visualiser le truc : quand on change t en -t, on conserve le même x, mais y change de signe)

si, les dl vont te donner une tangente : tu vas avoir le vecteur écrit à peu de chose près (les o(t²)) dans une base avec comme coordonnées t et t² : tu pourras représenter cette base, et utiliser les signes de t et t² pour savoir où se place M dans le repère

Moui, ça reste encore un peu flou mais je vais essayer

Rebonjour JAGC et Camelia
Je continue à répondre malgré tout sans relire tous ces messages. Il y aura peut être des doublons.
Je ne comprends pas ta courbe Camélia. En effet on a ici une cardioïde bien connue (voir sur google pour avoir une idée) On a une symétrie par rapport à Ox.  Ce n'est pas le cas  pour ton dessin.

Bon, j'ai du me tromper sur toute la ligne... Oubliez moi!