Bonjour

grâce à la périodicité, tu peux étudier sur un intervalle de longueur 2, mais cet intervalle, tu le places où tu veux.

Donc place le sur ]- ; ]
puis tu étudies la parité, et si elle est paire ou impaire, tu peux l'étudier seulement sur la moitié.
Oui ?

Mais lorsqu'elle est paire pour x et impaire pour y du coup qu'est ce au nous permet de réduire l'intervalle alors que c une symétrie par rapport à l'axe des abscisses.

Non, fais un croquis dans un repère
Tu vas obtenir une symétrie par rapport à...

Ox

Bonjour,

Je trouve un peu cavalier de nommer les fonctions x et y dans un repère qui semble être 0xy

la partie en gris c'est la courbe sur 0;pi
et en orange c est la courbe sur -pi;0

Bonjour,
Et si tu donnais les fonctions qui définissent x et y ?

OK
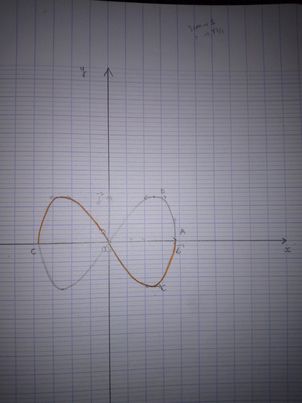
Soit M(t) le point de coordonnées x(t) et y(t).

M(t+2) = M(t)

M(-t) a pour coordonnées x(t) et -y(t).
Les points M(t) et M(-t) sont symétriques par rapport à l'axe des abscisses.

Est-ce plus clair ?

Bonjour,

aua, pourquoi écris-tu "x" sur l'axe des abscisses du graphe avec des fonctions:
x(t) = cos(t)  et y(t) = sin(2t) ?

Si le but était de faire le graphe de y=f(x) avec x et y données sous forme paramétrique (paramètre t), cela aurait était judicieux de le préciser dès le début.

Oui...quand on n'a pas d'énoncé complet dès le début, on peut répondre des choses fausses, incomplètes ou inexactes ....

Bonjour,

on ne peut pas définir une fonction f telle que y = f(x) avec (x, y) = (cos t ; sin 2t)
une fonction par définition fait correspondre à chaque valeur de x de son domaine de définition UNE valeur de y (pas deux)

le cercle d'équation cartésienne x²+y²=1 ne donne pas une fonction y = f(x) !
au mieux on peut représenter cet ensemble de point comme la réunion des graphes de plusieurs fonctions :

et

et c'est l'ensemble unique des points (x(t) = cos t; y(t) = sin t)
sans que appeler cela x, y ne choque qui que ce soit !

et si on est choqué (à tort ou à raison par une exarcerbation de rigueur) rien n'empêche de dire l'ensemble des points de coordonnées
x = f(t) = cos t et y = g(t) = sin t
ou simplement x = sin t, y = cos t

(ici dans l'exo y = g(t) = sin 2t)

d'accord je vois. Désolé pour ce manque de rigueur.

De rien et un bonus :
x(t) = cos(t)
y(t) = sin(2t)
M(t) le point de coordonnées (x(t) ; y(t)) avec t réel.
y(t) = 2sin(t)cos(t)
(y(t))² = 4sin²(t) (1-sin²(t))
M(t) et donc sur la courbe d'équation y² = 4x²(1-x²)
Réunion des représentations graphiques des fonctions f et -f avec
f(x) = 2x(1-x²).