Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre TopologieTopics traitant de topologie [tout]Lister tous les topics de mathématiques
Citation :
Quelle(s) condition(s) (suffisante) faut-il rajouter à l'ordre sur E pour qu'il en soit ainsi ?
Quelle(s) condition(s) (suffisante) faut-il rajouter à l'ordre sur E pour qu'il en soit ainsi ?
Si
On dit qu'un ensemble ordonné E est réticulé si toute paire d'élément de E admet une borne supérieure et une borne inférieure.
c'est le cas par exemple de
jsvdb @ 08-08-2019 à 18:22
On munit
de l'ordre suivant : (désolé, je n'arrive pas à faire un diagramme de Hasse en Latex sur l'
)
Alors![[1,7] \cap [2,8] = \{3,6\}](https://latex.ilemaths.net/ile_TEX.cgi?[1,7] \cap [2,8] = \{3,6\})
n'est pas un intervalle.
Citation :
Exercices :
Montrer que l'intersection de deux intervalles n'est pas toujours un intervalle.
Exercices :
Montrer que l'intersection de deux intervalles n'est pas toujours un intervalle.
On munit
)
Alors
L'exemple est faux :
Salut,
un exemple pour montrer que l'intersection de deux intervalles n'est pas toujours un intervalle.
Soit un réel strictement positif.
On défini dans la relation d'ordre
par
si et seulement si
et
Un dessin pour comprendre
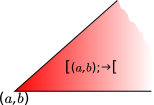
Il est graphiquement évident que c'est bien une relation d'ordre.
Et l'intersection de deux intervalles est un intervalle.
Considérons l'intersection des intervalles et
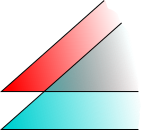
Un calcul simple montre que c'est l'intervalle
Maintenant on prend la restriction de cette relation à .
Si est irrationnel alors l'intervalle
n'est pas un intervalle de
muni de cette relation d'ordre bien que les intervalles
et
soient des intervalles de
Annuler
connectez vous
topologie en post-bac