Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Dérivée d'une fonction exo 1

Posté par
CloudNine 11-01-17 à 18:02

Bonsoir,
Je suis bloqué à certaines questions.
Exercice 1:     f(x) = x2 * (x2)*ln(x2)    si x est différent de 0
                              0   si x= 0

1) Vérifier que f est dérivable sur R et calculer f'

Comment vérifier que f est dérivable sur R ? Dois-je faire la limite du taux d'accroissement ?
lim (x-> 0-)  f'(x) = ( (f(x) - f(x0) ) / (x - x0)
lim (x->0-) f'(x) = ( x^2*ln(x^2)  - 0 ) / ( x - 0)
lim (x->0-) f'(x) = ( x^2*ln(x^2))   /  x
lim (x->0-) f'(x) = x*ln(x^2)
lim (x->0-) f'(x) = 2xln(x)
Or lim  (x->0) x*ln(x) = 0
Donc lim lim (x->0-) f'(x) = 2xln(x) = 0

Je suis bloqué ici, je ne vois pas comment déterminer la limite  à droite

(J'ai réussi à dérivé)

2) La fonction f est-elle deux fois dérivable sur R ?

Comment le montrer ?

Exercice 2: *****
Merci d'avance pour vos aides,

malou > 1 sujet = 1 exo ton autre exo est dans un 2e sujet ouvert à ton nom

Posté par
jsvdbre : Dérivée d'une fonction 11-01-17 à 18:04

Bonjour CloudNine

Si j'ai bien compris, f(x) = 2x^4\ln(x) avec f(0) = 0, c'est ça ?

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:06

Je rembobine :  f(x) = 2x^4\ln(|x|)

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 18:06

Bonsoir,
Je vous prie de vouloir m'excuser pour cette erreur que j'ai commise.
f(x) = x^2 * ln(x^2)

Posté par
verdurinre : Dérivée d'une fonction exo 1 11-01-17 à 18:25

Bonsoir,
tout d'abord f est dérivable sur R* comme produit  de fonctions dérivables.

En zéro, il faut effectivement calculer la limite du taux accroissement.

Mais ce que tu as fait s'applique sans utiliser l'hypothèse x<0.
Tu as donc écrit une démonstration correcte, à quelques fautes de frappes près.

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:32

Donc f(x) = 2x^2\ln(|x|) avec f(0) = 0

1) Effectivement, tu n'as pas le choix, tu dois voir deux choses :

- pour x > 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(x)

- pour x < 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(-x)

Et ces deux expressions tendent vers 0 en 0 donc f est dérivable en 0 et f'(0) = 0

Partout ailleurs, donc pour x \neq 0 : f'(x) = 4x(\ln(x^2) + 1), qui tend bien vers 0 en 0.

Donc f est continument dérivable, donc est C^1.

f est-elle deux fois dérivable :

- pour x \neq 0 : pas de soucis.

- pour voir si l'objet qu'on aimerait noter f''(0) existe ou pas, il faut alors regarder les deux mêmes choses dont je parle ci-dessus, mais avec f' à la place de f !

- pour x > 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

- pour x < 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

Enfin, en cas d'existence de f''(0), f''(x) existe alors sur \R et on peut en étudier la continuité. Si f'' est continue, alors f sera déclarée C^2 \\ .

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 18:43

Bonsoir,
Merci à verdurin

verdurin @ 11-01-2017 à 18:25

Bonsoir,
tout d'abord f est dérivable sur R* comme produit  de fonctions dérivables.

En zéro, il faut effectivement calculer la limite du taux accroissement.

Mais ce que tu as fait s'applique sans utiliser l'hypothèse x<0.
Tu as donc écrit une démonstration correcte, à quelques fautes de frappes près.


Merci, j'avais trouvé que f est dérivable sur R+* car ln(x) est dérivable sur R+* .  J'ai donc faux

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 18:44

jsvdb @ 11-01-2017 à 18:32

Donc f(x) = 2x^2\ln(|x|) avec f(0) = 0

1) Effectivement, tu n'as pas le choix, tu dois voir deux choses :

- pour x > 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(x)

- pour x < 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(-x)

Et ces deux expressions tendent vers 0 en 0 donc f est dérivable en 0 et f'(0) = 0

Partout ailleurs, donc pour x \neq 0 : f'(x) = 4x(\ln(x^2) + 1), qui tend bien vers 0 en 0.

Donc f est continument dérivable, donc est C^1.

f est-elle deux fois dérivable :

- pour x \neq 0 : pas de soucis.

- pour voir si l'objet qu'on aimerait noter f''(0) existe ou pas, il faut alors regarder les deux mêmes choses dont je parle ci-dessus, mais avec f' à la place de f !

- pour x > 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

- pour x < 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

Enfin, en cas d'existence de f''(0), f''(x) existe alors sur \R et on peut en étudier la continuité. Si f'' est continue, alors f sera déclarée C^2 \\ .


Merci beaucoup jsvdb, par curiosité qu'est-ce que '' C^1 ".  Je ne l'ai pas encore vu.  

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:49

Allez, en image.

Dérivée d\'une fonction exo 1

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:51

La dérivée :

Dérivée d\'une fonction exo 1

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:53

La dérivée seconde pour laquelle y'a un walou en 0 :

Dérivée d\'une fonction exo 1

Posté par
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 18:58

CloudNine @ 11-01-2017 à 18:44

qu'est-ce que '' C^1 ".  Je ne l'ai pas encore vu.  

Une fonction est dite avoir le caractère C^1 si elle est dérivable et que la dérivée est continue.
Dans cet exemple, ce n'est pas le cas. f'(0) existe. Certes il a fallu le calculer "à la main" et vérifier "à la main" que f' était continue en 0.

Une fonction est dite avoir le caractère C^2 si elle est deux fois dérivable et que la dérivée seconde est continue.
Dans cet exemple, ce n'est pas le cas. f''(0) n'existe même pas.

Voici un exemple de fonction dérivable sur \R mais non C^1 : j(x) = \dfrac{\sin(x)}{x} \text { avec } j(0) = 0

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 19:11

jsvdb @ 11-01-2017 à 18:32

Donc f(x) = 2x^2\ln(|x|) avec f(0) = 0

1) Effectivement, tu n'as pas le choix, tu dois voir deux choses :

- pour x > 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(x)

- pour x < 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(-x)

Et ces deux expressions tendent vers 0 en 0 donc f est dérivable en 0 et f'(0) = 0

Partout ailleurs, donc pour x \neq 0 : f'(x) = 4x(\ln(x^2) + 1), qui tend bien vers 0 en 0.

Donc f est continument dérivable, donc est C^1.

f est-elle deux fois dérivable :

- pour x \neq 0 : pas de soucis.

- pour voir si l'objet qu'on aimerait noter f''(0) existe ou pas, il faut alors regarder les deux mêmes choses dont je parle ci-dessus, mais avec f' à la place de f !

- pour x > 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

- pour x < 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

Enfin, en cas d'existence de f''(0), f''(x) existe alors sur \R et on peut en étudier la continuité. Si f'' est continue, alors f sera déclarée C^2 \\ .


Je pense que vous avez fait une erreur pour la dérivée.
Je trouve 2x(ln(x^2) +1)

Merci beaucoup mais je ne comprend pas la représentation graphique.
CloudNine,

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 19:11

jsvdb @ 11-01-2017 à 18:58

CloudNine @ 11-01-2017 à 18:44

qu'est-ce que '' C^1 ".  Je ne l'ai pas encore vu.  

Une fonction est dite avoir le caractère C^1 si elle est dérivable et que la dérivée est continue.
Dans cet exemple, ce n'est pas le cas. f'(0) existe. Certes il a fallu le calculer "à la main" et vérifier "à la main" que f' était continue en 0.

Une fonction est dite avoir le caractère C^2 si elle est deux fois dérivable et que la dérivée seconde est continue.
Dans cet exemple, ce n'est pas le cas. f''(0) n'existe même pas.

Voici un exemple de fonction dérivable sur \R mais non C^1 : j(x) = \dfrac{\sin(x)}{x} \text { avec } j(0) = 0


Merci beaucoup pour vos explications,

Posté par
CloudNinere : Dérivée d'une fonction exo 1 11-01-17 à 19:29

jsvdb @ 11-01-2017 à 18:32

Donc f(x) = 2x^2\ln(|x|) avec f(0) = 0

1) Effectivement, tu n'as pas le choix, tu dois voir deux choses :

- pour x > 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(x)

- pour x < 0 : \dfrac{f(x)-f(0)}{x-0} = \dfrac{f(x)}{x} = 2x\ln(-x)

Et ces deux expressions tendent vers 0 en 0 donc f est dérivable en 0 et f'(0) = 0

Partout ailleurs, donc pour x \neq 0 : f'(x) = 4x(\ln(x^2) + 1), qui tend bien vers 0 en 0.

Donc f est continument dérivable, donc est C^1.

f est-elle deux fois dérivable :

- pour x \neq 0 : pas de soucis.

- pour voir si l'objet qu'on aimerait noter f''(0) existe ou pas, il faut alors regarder les deux mêmes choses dont je parle ci-dessus, mais avec f' à la place de f !

- pour x > 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

- pour x < 0 : \dfrac{f'(x)-f'(0)}{x-0} = \dfrac{f'(x)}{x} = ...

Enfin, en cas d'existence de f''(0), f''(x) existe alors sur \R et on peut en étudier la continuité. Si f'' est continue, alors f sera déclarée C^2 \\ .


Voilà ce que j'ai fait pour la 2)
Pour x > 0 : ( f'(x) - f'(x0) ) / (x - x0) = 2ln(x)
Pour x < 0:  ( f'(x) - f'(x0) ) / (x - x0) = 2ln(-x)
lim (x-> 0-) f''(x) = lim x-> 0+ f''(x) = -oo
Donc f n'est pas deux fois dérivable.  

Posté par
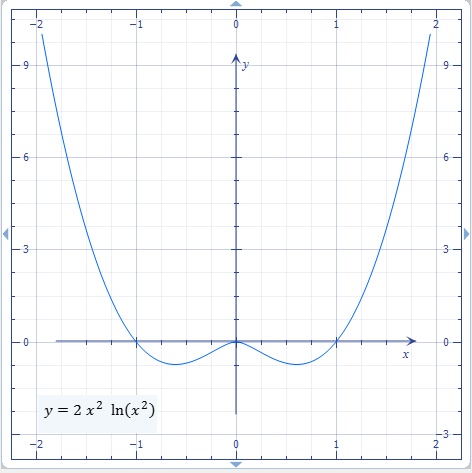
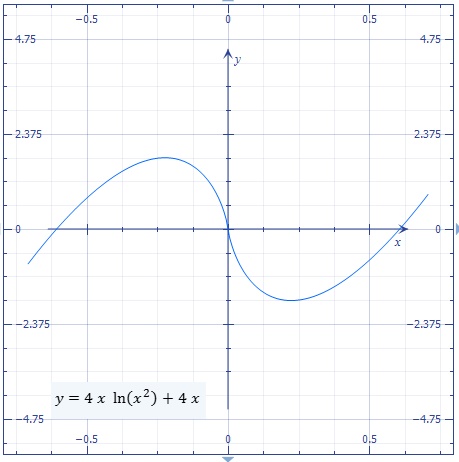
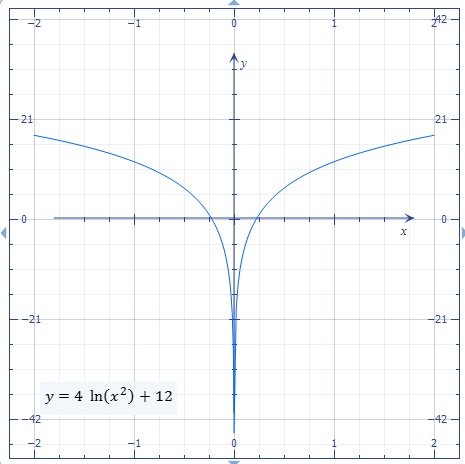
jsvdbre : Dérivée d'une fonction exo 1 11-01-17 à 19:47

Il ne faut pas se compliquer la vie :

( f'(x) - f'(0) ) / (x - 0) = f'(x) / x = 4(\ln(x^2)+1) pour tout x 0 qui tend vers - en 0.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !