- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
déterminer l'image de f
Bonjour,
Je dois déterminer l'image de f avec
f(z) = (2iz) / (z + 1), |z| < 1
J'ai essayé de simplifier en multipliant par z(bar) + 1 mais après simplification, l'expression reste assez compliquée..
Merci pour votre aide.
Bonjour ThierryPoma.
Tu as écrit et il me semble que c'est plutôt
.
Et la minoration de que tu proposes est alors moins facile à utiliser.
Sauf erreur, je pense (mais ne vois aucun moyen de l'expliquer simplement sans l'utilisation de "vieilles" transformations géométriques) que l'image du disque serait un demi-plan ouvert ayant un bord parallèle à l'axe réel...
Un essai : donc
(évidemment,
)
Alors soit
.
Mais je n'ai pas la condition suffisante. Si tu vois...
Bonjour Luzak,
Bonjour ThierryPoma.
Tu as écrit
Et la minoration de
Très juste... Je deviens vieux.

Bonjour,
On trouve: si
avec égalité sur le cercle.
Bon, ça ne prouve toujours pas que tout le demi plan est atteint...

J'ai fait une erreur : c'est bien et non pas ce que j'ai indiqué.
Une condition suffisante :
On a toujours .
La fonction réciproque de est
Et on a lorsque
Bonjour à tous.
Effectivement, Luzak, prendre de "vieilles transformations géométriques pour commencer, me semble pas mal.
En fais, le problème posé est équivalent à celui-là : prendre l'image du disque par l'application
.
Autrement dit, si , il suffira, à partir de
d'effectuer les transformations suivantes :
(symétrie centrale)
(translation)
(rotation d'angle
)
(homothétie de centre 0 et de rapport 2)
Maintenant, le plus dur est de trouver . Et là, on a plusieurs solutions. Soit par des arcs de cercle, soit par des segments ouverts.
J'explicite ce que j'entends par "segments". Il est vivement conseillé de faire un dessin au fur et à mesure.
.
.
.
(Cela fait deux segments dont on connait l'image par
).
Du coup on obtient : .
Et maintenant, à , on applique les 4 transformations décrites ci-dessus.
Au final, sur le plan, on obtient l'image cherchée qui ressemble à une grande chauve-souris dont il manquerait la tête et qui volerait vers le haut du plan (s'il est orienté de façon traditionnelle).
Plus analytiquement, on a "presque" tout le plan et une "petite" partie de
(qui doit être limitée par la droite
.
Tout est bien sûr à vérifier.
salut
je suis de loin et en voyant le dernier msg de jsvdb il me vient l'idée suivante :
l'image du disque unité ouvert est l'union des images des cercles de rayon r avec r < 1
...
Salutations Carpediem.
Exactement, sauf que ça ne m'inspirait pas des masses de travailler avec avec
et
.
Ça aurait dû, ou ptet pas ! 
Bonjour tous les deux !
J'ai mis "utilisation de transformations géométriques" pour dire ce qui m'a suggéré la solution.
Ceci dit il n'est pas difficile de prouver que transforme le cercle de diamètre
en droite.
En polaires le cercle a pour équation et l'image par
a donc pour équation
.
On peut alors mettre des inégalités et prouver la propriété voulue pour le disque ou, comme le suggère carpediem, réunir des cercles tangents en à l'axe imaginaire (cela me semble plus simple que de prendre des cercles concentriques)...
bonjour,
En posant je retrouve les transformations données par jsvdb
mais ne vois pas de chauve-souris

disque de centre z= 1 et de rayon r= 1 privé de l'origine du repère.
Il me semble que en remarquant que peut être aussi proche de 0 que désiré , par inversion (
le point
peut être "envoyer à l'infini sur la demi droite ]OM')
comme le Disque est tangent à (oy) en O, je pense que
est le demi plan ouvert Re(Z)>0
ensuite avec la symétrie de rapport -1 suivie de la translation de vecteur U=1 puis la rotation de centre O et d'angle et enfin l'homothétie de centre O et de rapport 2 on obtient pour image définitive le demi plan ouvert Im(z)>2
En reprenant la Luzak's idea :
On cherche l'image du disque ouvert D de diamètre par
.
Ce disque est la réunion disjointe des cercles
Il vient .
Donc
Donc
Et en faisant mes transformations successives l'image cherchée est
Ma chauve-souris, elle s'est écrabouillée. Et vlan le batman !
bonsoir,
J'espère être un peu plus fiable, L'intersection du cercle unité et du cercle de centre z=1 et de rayon 1 est constitué de deux points A et B or ces points sont échangés par la transformation z'---> comme l'image d'un cercle par une inversion dont le centre est sur le cercle est une droite , l'image du cercle de centre z+1 et de rayon 1 est la droite (AB) d'équationX=1/2 il me semble alors qu'il faut corriger ma première désastreuse intervention en remplaçant le demi-plan R(Z)>0 par R(Z)>1:2
L'image définitive serait donc sauf erreur le demi plan Im(z)>1
re,
en effet alors ? sans doute parce que tu as supposé Z différent de 0 dans ta transformation, et moi j'ai supposé z' différent de 1, il faut donc ajouter le point O dans l'image trouvée
D'ailleurs M'(1) est fixe par I: Z---> I(Z+1)=Z+1 ce qui donne bien pour z=0 I(1)=1
non, en fait il y a une faute de frappe dans mon post :
Et en faisant mes transformations successives l'image cherchée est
@ jsvdb
Je reprends ton message de 16h38.
Quand tu dis tu donnes un ensemble de réels.
Pour les cercles il faudrait mettre .
Le problème dans ce cas (j'étais tombé sur le même os) c'est le passage à l'inégalité pour le disque qui serait . Il faudrait, pour être cohérent que
aient même argument ce qui n'est pas le cas si tu ne prends pas
(la symétrie par rapport à l'axe réel ne gêne pas car les parties envisagées sont invariantes par cette symétrie).
On aurait alors le disque décrit par et, comme
il vient
Oui effectivement, tu as raison, je dois mettre plus de rigueur dans ma rédaction !
Déjà, je pense que l'ensemble à trouver doit être le bon.
Je vais revoir tout ce que tu as dit, mais à tête reposée ...
bon je vais clore le débat ....
après une étude sur geogebra ....et "2h" de calcul dont la moitié faux c'est pourquoi ça m'a pris tout ce temps fait iech la vie
je vous passe les calculs ... mais à vous de vérifier ... 
soit
l'image du cercle |z| = r est le cercle de centre w et de rayon R
ouf .... 
reste à préciser ce qui se passe quand r tend vers 1 ... 
Carpe : Luzak et ton serviteur ont déjà clos le débat :
il vient
Et en faisant mes transformations successives l'image cherchée est

bonjour,
Je traite géométriquement le problème
Comme je l'ai écris avant , j'ai pris le parti de changer de variable en posant z'=z+1
donc l'expression de f(z) devient
la contrainte devient donc appartient au disque ouvert de centre I(1) et de rayon1 Il s'agit de déterminer l'image de ce disque par
cette transfiormation se décompose en
autrement dit la composition
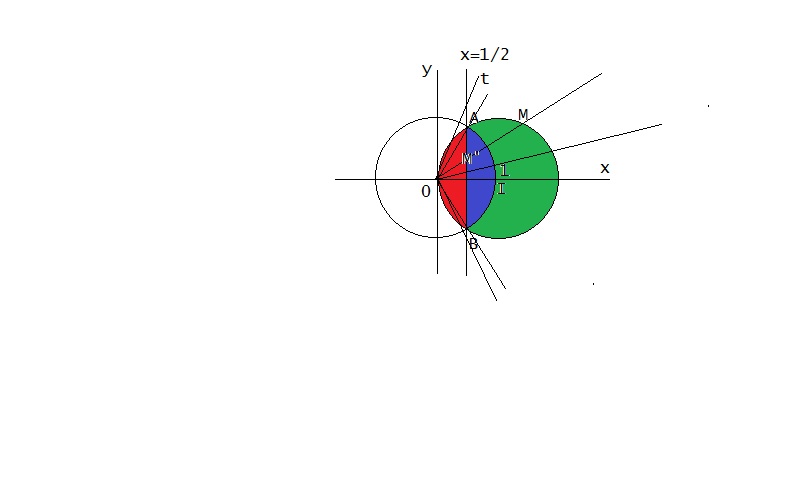
le cercle de centre I et de rayon 1 a pour image la droite d'équation x=1/2 car l'image d'un cercle par une inversion dont le centre est sur le cercle est une droite.
or A et B sont échangés par cette inversion donc l'image est la droite (AB)
L'arc AIB est globalement fixe , la zone intérieure verte est envoyé sur la lunule bleu ; la zone intérieure rouge sur le complémentaire des zones bleues et rouge du demi-plan x>1/2
Ainsi l'image par g du disque ouvert de centre I(1) et de rayon 1 est le demi plan ouvert de frontière x=1/2
Pour information quand la demi-droite Ot tend vers (oy) , un point correspondant du cercle de centre I et de rayon 1 a pour image un point de x=1/2 et un point intérieur a son image dans le demi plan .
Si ensuite on applique dans l'ordre les autres transformations on obtient successivement : le demi plan ouvert symétrique x<-1/2 puis le demi-plan ouvert y<1
et c'est là que je me suis égaré au post précédent.
remarque sur la figure ce n'est pas M" qui est l'image de M mais son symétrique /ox


 analyse complexe en post-bac
analyse complexe en post-bac