- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Déterminer un domaine de C
Bonjour,
Cela fait maintenant trois semaines que je planche sur un sujet sans succès. De ce fait, j'aimerais avoir une (ou plusieurs) piste de recherche pour le résoudre.
Mon problème est le suivant :
Je cherche à démontrer qu'un domaine (ouvert connexe) de
tel que
est égal à
(ou au moins biholomorphe à ce dernier).
Merci d'avance pour votre aide. 
Salut,
pas facile comme exercice....
Je propose une piste: Prendre une boule ouverte B( ,r)\{
,r)\{ } en considérant une fonction holomorphe avec une singularité essentiel en
} en considérant une fonction holomorphe avec une singularité essentiel en  ; et en utilisant le théorème suivant:
; et en utilisant le théorème suivant:
Soit f dans B(a,r)\{a} une fonction holomorphe avec une singularité essentiel en a. Soit T={c
 /
/  (zn)n, zn
(zn)n, zn a et limn
a et limn zn=a, f(zn)=c
zn=a, f(zn)=c  n}
n}
Alors soit T= , soit T=
, soit T= \{w} pour UN SEUL w
\{w} pour UN SEUL w
 .
.
L'idée est ensuite de prouver que w= et que le premier cas n'est pas possible;ce qui est loin d'être facile je le conçois...( ce n'est d'ailleurs peut être pas possible avec les maigres hypothèses que l'on a mais ça reste une piste)
et que le premier cas n'est pas possible;ce qui est loin d'être facile je le conçois...( ce n'est d'ailleurs peut être pas possible avec les maigres hypothèses que l'on a mais ça reste une piste)
soit D un ouvert connexe de frontière {a}
toute demi-droite d'origine le point A d'affixe a s'écrit avec r > 0 et t réel positif ...
si D est borné ou plus précisément si D est inclus dans un quelconque demi-plan de frontière la droite d alors il existe un réel t tel que z appartienne à la frontière de D
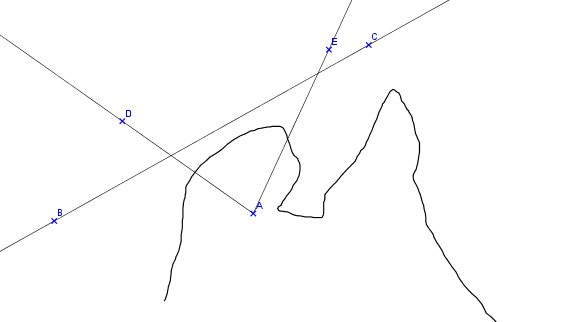
une image pour comprendre ce que je veux dire : si la droite (BC) borne le domaine D alors les demi-droites [AD) et [AE) coupent la frontière de D
à mettre peut-être mieux en forme pour montrer qu'on la frontière contient au moins deux points si D est borné ""suivant une direction""
par contraposée on prouve donc que D n'est pas borné ...
saalut
peut-être montrer que ce domaine n'est pas borné dans aucune direction autour de a ...
J'y avais penser mais sans grand succès. (C'est peut-être faisable mais je n'est pas encore trouvé comment)
soit D un ouvert connexe de frontière {a}
toute demi-droite d'origine le point A d'affixe a s'écrit
si D est borné ou plus précisément si D est inclus dans un quelconque demi-plan de frontière la droite d alors il existe un réel t tel que z appartienne à la frontière de D

une image pour comprendre ce que je veux dire : si la droite (BC) borne le domaine D alors les demi-droites [AD) et [AE) coupent la frontière de D
à mettre peut-être mieux en forme pour montrer qu'on la frontière contient au moins deux points si D est borné ""suivant une direction""
par contraposée on prouve donc que D n'est pas borné ...
J'ai réussi à démontrer par votre méthode que D n'est pas borné mais je n'ai pas encore réussi à démontrer que D n'est borné selon aucune direction (je vais tenter de le faire après ce post
 )
)
Salut,
pas facile comme exercice....
Je propose une piste: Prendre une boule ouverte B(
 ,r)\{
,r)\{ } en considérant une fonction holomorphe avec une singularité essentiel en
} en considérant une fonction holomorphe avec une singularité essentiel en  ; et en utilisant le théorème suivant:
; et en utilisant le théorème suivant:
Soit f dans B(a,r)\{a} une fonction holomorphe avec une singularité essentiel en a. Soit T={c

 /
/  (zn)n, zn
(zn)n, zn a et limn
a et limn zn=a, f(zn)=c
zn=a, f(zn)=c  n}
n}
Alors soit T=
 , soit T=
, soit T= \{w} pour UN SEUL w
\{w} pour UN SEUL w
 .
.
L'idée est ensuite de prouver que w=
 et que le premier cas n'est pas possible;ce qui est loin d'être facile je le conçois...( ce n'est d'ailleurs peut être pas possible avec les maigres hypothèses que l'on a mais ça reste une piste)
et que le premier cas n'est pas possible;ce qui est loin d'être facile je le conçois...( ce n'est d'ailleurs peut être pas possible avec les maigres hypothèses que l'on a mais ça reste une piste) Le problème avec votre méthode c'est qu'elle demande un théorème de la théorie des singularités (je crois
 ) et que cette théorie n'a été évoquée qu'en surface dans mon cours de fonction holomorphe. Sachant que j'ai besoin de ce résultat dans le cadre d'un stage, cela rajouterai un énoncé que je devrais démontrer.
) et que cette théorie n'a été évoquée qu'en surface dans mon cours de fonction holomorphe. Sachant que j'ai besoin de ce résultat dans le cadre d'un stage, cela rajouterai un énoncé que je devrais démontrer.
D'ailleurs, pour un peu de mise en contexte, j'ai besoin de ce résultat pour démontrer que si on ajoute une hypothèse de simple connexité à D et qu'on retire l'hypothèse sur
J'ai également essayer de démontrer que
Bonsoir,
on peut aussi prendre un point x dans le complémentaire DC de D.
Et remarquer que si B est une boule ouverte de centre x incluse dans DC alors B {
{ } est un fermé.
} est un fermé.
encore plus simple peut-être :
soit t réel fixé, d = {z = raexp (it) / r > 0} la demi-droite d'origine a dans la direction angulaire t et E = d  D
D
alors tout simplement si E  d alors les les éléments de
d alors les les éléments de  E sont des éléments de
E sont des éléments de  D différents de a
D différents de a

la demi-droite d = [AB) rencontre D et ici E= ]a, X]  [Y, Z]
[Y, Z]  [W, B) et les points X, Y, Z et W appartiennent à la frontière de D
[W, B) et les points X, Y, Z et W appartiennent à la frontière de D
PS : les points X, Y, ... ne sont pas marqués ...
encore plus simple peut-être :
soit t réel fixé, d = {z = raexp (it) / r > 0} la demi-droite d'origine a dans la direction angulaire t et E = d
 D
D
alors tout simplement si E
 d alors les les éléments de
d alors les les éléments de  E sont des éléments de
E sont des éléments de  D différents de a
D différents de a

la demi-droite d = [AB) rencontre D et ici E= ]a, X]
 [Y, Z]
[Y, Z]  [W, B) et les points X, Y, Z et W appartiennent à la frontière de D
[W, B) et les points X, Y, Z et W appartiennent à la frontière de D
PS : les points X, Y, ... ne sont pas marqués ...
Ce n'est peut-être pas la méthode la plus simple ni la plus rapide mais grâce à votre idée j'ai finalement trouvé une démonstration.
J'aimerais d'ailleurs avoir votre avis dessus, la voici :
Pour
De votre indication (je passe les détails du calcul) on peut montrer que
De ce fait
De plus,
En utilisant le fait que
De plus
On conclut par connexité de
Bonjour.
En reprenant toutes les idées, tu montres simplement que la boule et ce pour tout
.
Tu le montres en disant que ce c'est pas le cas alors il y a un tel que
et tu considères le segment
qui rencontre alors la frontière de
.
Bon en fait, c'est pas suffisant.
Il faut commencer par dire que (car D étant ouvert, il ne pourrait pas être sur la frontière) et est adhérent à
(car il est sur la frontière)
Donc il existe une suite de points de points de
qui converge vers
.
Pour chacun de ses points, il existe une suite telle que
et
Et là tu reprends ma démo :
Soit avec
et
Alors tu trouveras forcément un point dans une des boules
tel que
et donc le segment
rencontrera
en point différent de
Conclusion : toute boule et
je ne comprends pas toutes ces histoires de suites et sous-suites ...
mais effectivement c'est mon idée en plus concis ... et mieux formalisée ...
on considère les sphères avec r > 0
si pour un certain r alors il existe un complexe z <> a de cette intersection qui appartient à la frontière de D (puisque D est ouvert)
je ne comprends pas toutes ces histoires de suites et sous-suites ...
mais effectivement c'est mon idée en plus concis ... et mieux formalisée ...
on considère les sphères avec r > 0
si pour un certain r alors il existe un complexe z <> a de cette intersection qui appartient à la frontière de D et pas à D (puisque D est ouvert)
Oui mais cette fois c'est trop concis car il faut préciser qu'on prend un r pour lequel l'intersection est non vide et préciser que si l'intersection est vide alors on peut trouver un r plus petit pour lequel l'intersection est non vide.
Ensuite rien ne nous garantit que l'on puisse trouver un r tel que L'intersection soit différente de Sr.
Si on est dans un tel cas alors D était en réalité une boule ( sauf son centre a) et on sait que la frontière d'une boule n'est pas réduite à un point .
Enfin après avoir éliminé tous ces cas alors effectivement c'est ton raisonnement qui s'applique.
Dans  il y a 3 ouverts ayant {0} pour frontière .
il y a 3 ouverts ayant {0} pour frontière .
Dans un  -evn E de dimension > 1 il n'y a que E\{0} :
-evn E de dimension > 1 il n'y a que E\{0} :
On utilise les propriétés suivantes :
1.Les ouverts connexes de  sont les intervalles ouverts ]a , b[ ( -
sont les intervalles ouverts ]a , b[ ( -
 a
a  b
b  +
+ )
)
2.Les composantes connexes d'un ouvert de  sont des ouverts ( donc des intervalles ouverts )
sont des ouverts ( donc des intervalles ouverts )
3.Pour tout (x,y)  E² tel que x
E² tel que x  y , t
y , t  x + t(y - x) réalise un homéomorphisme de
x + t(y - x) réalise un homéomorphisme de  sur la droite D(x,y) "passant par x et y " .
sur la droite D(x,y) "passant par x et y " .
Soit donc U un ouvert de E n'ayant que 0 pour point frontière . U est donc non vide . Soient a  U et
U et  := { t.a | t
:= { t.a | t  1 } (c'est la demi-droite fermée contenant 0 et d'extrêmité a ) .
1 } (c'est la demi-droite fermée contenant 0 et d'extrêmité a ) .
Soit x  E \
E \  .
.
U D(a,x) est un ouvert de la droite D(a,x) contenant a . La composante connexe
D(a,x) est un ouvert de la droite D(a,x) contenant a . La composante connexe  de U
de U D(a,x) contenant a est donc un "segment " ouvert contenu dans D(a,x) . Si on avait
D(a,x) contenant a est donc un "segment " ouvert contenu dans D(a,x) . Si on avait 
 D(a,x) une de ses extrémités serait un point fronntière de U . On a donc D(a,x)
D(a,x) une de ses extrémités serait un point fronntière de U . On a donc D(a,x)  U .
U .
Par suite U contient E \  .
.
Si U  E \ {0} il existe b
E \ {0} il existe b 
 tel que b
tel que b  U . b est alors point frontière de U .
U . b est alors point frontière de U .
Comme ce n'est pas le cas on a U = E \ {0} .
Rq : Je n'ai pas supposé que U était connexe .
Merci etniopal  je ne m'étais même pas demandé si le résultat se généralisait mais je suis content de voir que oui
je ne m'étais même pas demandé si le résultat se généralisait mais je suis content de voir que oui 
ouais ben c'est exactement ce que je dis (à 12h33) ... en plus symbolique ... avec rigueur et méthode comme à son habitude ...
effectivement tout provient des propriétés de et de ses connexes ...
pour tout z dans U = E - {a} on note D la demi-droite [a, z)
si l'ensemble U  D n'a pas exactement une composante connexe alors la frontière de U contient un deuxième point ... ce qui contredit l'hypothèse ...
D n'a pas exactement une composante connexe alors la frontière de U contient un deuxième point ... ce qui contredit l'hypothèse ...
à noter comme l'a fait etniopal que l'hypothèse U connexe est inutile au raisonnement ... ce que j'avais remarqué dès le début ... (mais évidemment si U n'est pas connexe c'était immédiatement fini)


 analyse complexe en post-bac
analyse complexe en post-bac