x1 = (3-racine 25)/2 = (3-5)/2 = -1

x2 = (3+racine 25)/2 = (3+5)/2 = 4 ??

Oulah je crois c'est à cause de l'heure tardive mais tu mélanges tout là...

Resolvons d'abord



Donc g'(x)=0 ,pour x=-1 et x=1.

Maintenant il faut faire le tableau de signe de g'(x) :


x          -                    -1                1              
g'(x)                  ???          0     ???      0       ???

Et la tu dois remplacer les ??? soit par + ou par - en fonction du signe de g'(x)

Ah mais oui g'(x)=0 je l'avais résolu mais en faite je n'avais pas compris de quel solution vous parlé.

Et pour le tableau c'est +  -  +

Oui c'est ça

Pour ,, donc g est croissante
Pour ,, donc g est décroissante
Pour ,, donc g est croissante

Comme tu peux le voir se le graphique ci dessous

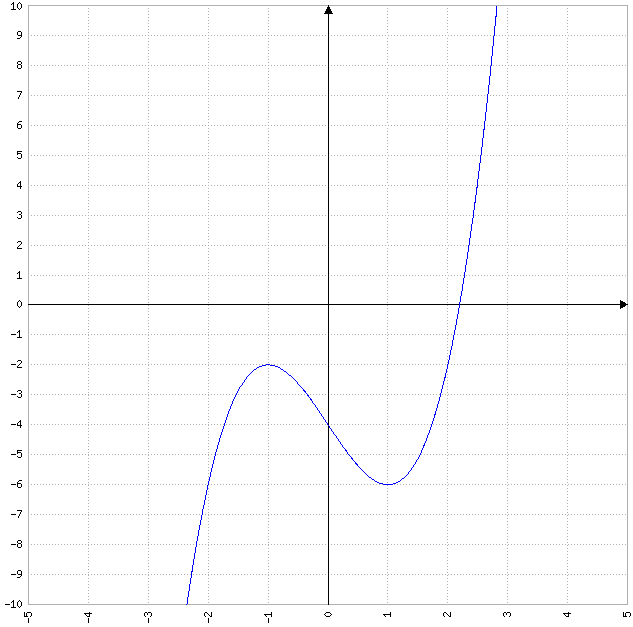
Oui désolé pour la confusion j'avais calculer les racines de delta.

Et du coup on peut en conclure que g(x) est croissante ? Puisque au départ c'est d'elle que je doit dresser le tableau de Variation.

lol non elle est croissante pour tout les x tels que g'(x) > 0 ( sur le graphique tu peux pas dire qu'elle est croissante )

Du coup en terminale t'as bien vu les racines les discriments etc etc non ,?

:o:o:o:o:o:o:o:o

Regarde juste mon dernier post j'ai tout mis dedans la fonctions tu trouves qu'elle est toujours croissante?!?

enfin je devrais dire elle est croissante sur les emsembles tel que g'(x) > 0

A partir du moment où il a quelque point qui sont décroissante on peu plus la qualifier de croissante ??

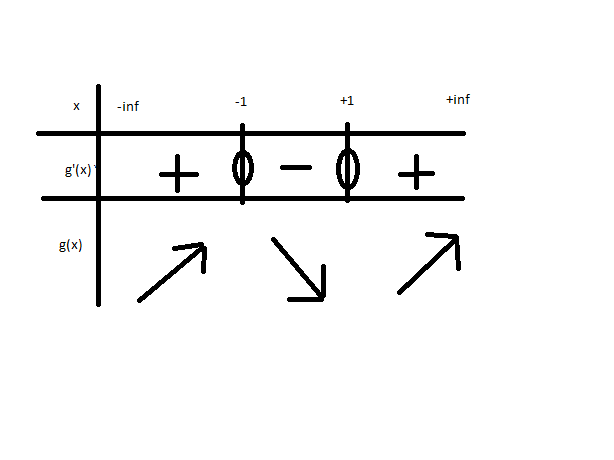
Mais donc a quoi ressemble mon Table de variation de g(x) ?

           x    /infty       -1           1          +/infty
signe de g(x)    ???         ???         ???            ???

Et bien sur , donc g est croissante sur

Elle est ensuite décroissante sur, puis ensuite elle est croissante sur

Donc ta fonction g est croissante, puis décroissante, puis croissante

Une fonction n'est pas toujours soit croissante, soit décroissante, elle peu faire les deux comme ici regarde le tracé de la courbe que j'ai posté tu vois que la courbe monte, descend puis monte (croissante,décroissant,croissant)

Prend l'habitude de dire croissante sur un intervalle , en effet sur tout l'intervalle la fonction n'est ni croissante ni décroissante elle est rien du tout ! , de plus ne parle pas de la croissance en un point mais bien sur un intervalle , la il faut dire elle est croissante sur moins l'inifini -1 puis decroissante sur -1 1 puis croisssante sur 1 + l'infini

Daccor, et bin j'aurais apris pas mal de chose en une soirée merci à vous 2.

Je vais me couché parce que sa sert plus trop a grand chose de continuer a une heure pareil, je le continuerai plus tard Merci encore =)

Voila en gros ce que tu dois avoir c'est le tableau de signe de g'(x) et le tableau de variation de g(x)

Bonjour, Donc pour les variation de g(x): croissant de -infini a -2, décroissant de -4 à -6 et croissant de -2 a +infini
(Je parle bien de g(x) et non des valeur de x ^^)

Bonjour j'aurais besoin d'aide pour résoudre g(x)=0 je sais qu'alpha est compris entre 2 et 3.
0= x^3 - 3x - 4

est compris entre 2 et 3 on calcule par dichotomie
g(2)=8-6-4=-2
g(3)=27-9-4=12
on calcule g(2.5)=4.625
donc la racine est compris entre 2 et 2.5
on calcule g(2.25)....

Oui j'ai fait plusieur calculs "test" c'est vers 2,2... mais il c'est la seulefason de résoudre g(x)=0 ? Juste en faisant des "tests" ?

Car dans la question je doit montrer que l'équation g(x)=0 admet une seule solution sur R, puis ensuite déterminer alpha grace à la calculette:

La plus proche que je trouve est 2.19583 pour 2.19584 passe négatif, donc arondie à 10^-2 cela donne comme solution 2.20 mais comment demontrer qu'elle est la seule solution sur R ?

Ah ! Peut être en utilisant le tableau de variation de g(x), g(x) est croisant sur l'interval ]-infini;-1[ ses valeur sont -infini ; -6 puis g(x) et décroissant sur ]-1;1[ donc n'attein pas 0 et croissant sur ]1; + infini[ là g(x) admet une varleur 0 puis grimpe jusqua des valeurs infini donc elle ne repasse pas par 0.

Ma démarche n'est pas au top :s

On te demande une valeur approchée pas la valeur exacte donc le plus rapide c'est par dichotomie ou la calculette programmée

Je suis bloqué a la question 3) parti B:

Il suffi juste de faire un tableau de signe ?

    Tu en es où , maintenant ?...  Car dans ton problème -fleuve (comme les romans-fleuves), on perd complétement le fil du raisonnement ...

    

Alors je me suis débloqué, à présent j'en suis a la question 1 parti C je vais vous expliquez ce que j'ai fait

Parti C:

1) f(x) = (x^3 + 2x²)/(x²-1)

f= u/v            f'= (u'v-uv')/v²

u= x^3 +2x²       u'= 3x² + 4x

v= x²- 1          v'= 2x

f'(x) = (3x²+4x)(x²-1) - [(x^3+2x²)2x]  le tout sur v²=(x²-1)²
f'(x) = (x^4 -3x² -4x)/(x²-1)²
f'(x) = (x(x^3 - 3x -4))/ (x²-1)²
f'(x) = (xg(x))/(x²-1)²

Jusqu'ici tout va bien, enfin je croi ...

Mais ensuite je doit dresser le tableau de variation de f donc le tableau de signe de f' mais je m'embrouille avec ce que je doit metre dedans:

x                -infini    -1     1     2.2     +infini
signe de f'(x)       +      ||  0  ||  -  |0     +
Variation             ?????????????????????????????

Désolé mon tableau est décalé + en dessous de infini les 2 || sont en dessosude  -1 et 1 et ect

Il n'y a vraiment personne qui puisse m'aider ? Cela fait déjà plusieur que je suis bloqué :

Bonsoir après mainte demande personne ne vien plus sur mon post qui date de plusieur jours déjà Devoir Maison TS fonctions

J'en était a la Question 1 parti C donc je disait:

1) f(x) = (x^3 + 2x²)/(x²-1)

f= u/v            f'= (u'v-uv')/v²

u= x^3 +2x²       u'= 3x² + 4x

v= x²- 1          v'= 2x

f'(x) = (3x²+4x)(x²-1) - [(x^3+2x²)2x]  le tout sur v²=(x²-1)²
f'(x) = (x^4 -3x² -4x)/(x²-1)²
f'(x) = (x(x^3 - 3x -4))/ (x²-1)²
f'(x) = (xg(x))/(x²-1)²

Jusqu'ici tout va bien, enfin je croi ...

Mais ensuite je doit dresser le tableau de variation de f donc le tableau de signe de f' mais je m'embrouille avec ce que je doit metre dedans:

x                    -infini    -1     1     2.2     +infini
signe de f'(x)       +      ||  0  ||  -  |0     +
Variation             ?????????????????????????????

Le tableau doit vien ressembler a ceci ?

Je m'escuse par avance pour se "multi-post"

*** message déplacé ***
_{* Océane > pose toutes les questions de ton exercice dans le même topic mxo, merci *
Je m'excuse par avance pour ce ban}

Bonjour deadinsoul

Mais c'est un vrai multi-post et tu as eu de l'aide sur le topic en question...
Hier, déjà, tu es subitement intervenu dans un topic où je participais pour me demander de l'aide.

Comme j'ai pu constater que tu en avais reçu, j'ai laissé ce topic aux mains des aidants de Devoir Maison TS fonctions  

*** message déplacé ***