Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

différence d'exponentielles

Posté par
jbsph 30-11-23 à 22:15

Bonjour, savez-vous comment montrer que :
(e^(inx) - e^(ipx))^2  = 2-2cox((n-p)x) ?
n,p   et x est dans 0, 2*pi

Posté par
GBZMre : différence d'exponentielles 30-11-23 à 22:23

Rebonsoir,,
Ça ne serait pas plutôt

\large \left| e^{inx}-e^{ipx}\right|^2=2-2\cos((n-p)x) ?

Posté par
Sylvieg Moderateurre : différence d'exponentielles 01-12-23 à 08:19

Bonjour,
Merci jbsph de mettre à jour ton niveau dans ton profil.

Posté par
jbsphre : différence d'exponentielles 01-12-23 à 08:21

Si, pardon c'est ça, en module

Posté par
Sylvieg Moderateurre : différence d'exponentielles 01-12-23 à 08:25

OK

Posté par
jbsphre : différence d'exponentielles 01-12-23 à 09:04

Bonjour, profil mis à jour

Posté par
GBZMre : différence d'exponentielles 01-12-23 à 09:25

Il y a un truc qui revient souvent pour les sommes ou différences de nombres complexes de mosule 1 :

\Large e^{ia}\pm e^{ib}= e^{i(a+b)/2}\left(e^{i(a-b)/2}\pm e^{-i(a-b)/2}\right)
et ensuite se souvenir du lien entre les fonctions trigonométriques de (a-b)/2 et ce qui est entre parenthèses dans le terme de droite.

Posté par
GBZMre : différence d'exponentielles 01-12-23 à 09:27

Ou ici, on peut plus simplement se souvenir que |z|^2=z\overline z.

Posté par
Pirhore : différence d'exponentielles 01-12-23 à 10:12

Bonjour,

je ne fais que passer!

GBZM @ 01-12-2023 à 09:27

Ou ici, on peut plus simplement se souvenir que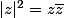 |z|^2=z\overline z.

je l'ai résolu de cette manière et dans ce cas précis, c'est plus rapide

Posté par
jbsphre : différence d'exponentielles 01-12-23 à 10:51

Super, j'ai fait les deux méthodes (qui ne demandent pas de connaître les mêmes formules trigo ^^).
Merci pour vos réponses!

Posté par
GBZMre : différence d'exponentielles 01-12-23 à 11:11

Avec plaisir.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !