Inscription / Connexion Nouveau Sujet
Différences Divisées
Bonjour,
J'aurai besoin de votre aide, j'ai du mal a faire un exercice :
On considère une subdivision régulière {x0, . . . , xn} de l'intervalle [a, b] avec x0 = a, xk = x0 + k
x et x = (b − a)/n.
Calculer les différences divisées suivantes : f[x0], f[x0, x1], f[x0, x1, x2] et f[x0, x1, x2, x3].
f[x0] = f(a)
f[x0, x1] = (f[x1] - f[x0]) / (x1 - x0)
...
En fait je ne sais pas s'il est possible de donner une vrai valeur pour f[x1] en faisant :
f[x1] = f(a + (b − a)/3) = f(a) + 1/3(f(b)-f(a)) = 2/3f(a) + 1/3f(b)
Mais pour que cela fonctionne il faut que f soit une application linéaire et j'en doute... Sinon je laisse simplement les f[x0], f[x1] ect... Sans les simplifier ?
Merci.
Bonjour, 
Vraiment idiot comme exercice...Je dirais : Fait comme tu le sens ! 
Tu peux seulement dire :
Oui je pense qu'en fait c'est seulement pour s'initier à la seconde question qui est une démonstration :
Montrer par récurrence que :
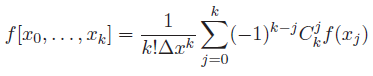
Une petite aide serait très précieuse, je bloque depuis...
Donc moi j'ai fais :
- Pour n = 0, l'hypothèse de récurrence est vérifiée.
- Supposons vrai :
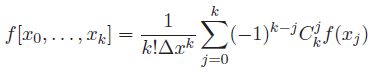
Montrons-le au rang supérieur, c'est-à-dire au rang n+1 :
f[x0,...,xk+1] = (f[x1,...,xk+1] - f[x0,...,xk]) / (xk+1 - x0)
=
A = 
j=1k+1 E
B = j=0k E
E = (-1)k-j Ckj f(xj)
Avec les données ci-dessus, on a :
f[x0,...,xk+1] = [A - B]
Je trouve :
[A - B] = Ek+1 - E0
Je ne devrais pas trouver cela...
Aidez-moi s'il vous plaît.
Merci.
Annuler
connectez vous
analyse en post-bac