Annuler
connectez vous
- Arithmétique : divisibilité, PGCD et PPCM, Nombres premiers
- Des mathématiciens célèbres : Fermat et Gauss
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale ArithmétiqueTopics traitant de Arithmétique [tout]Lister tous les topics de mathématiques
Niveau terminale
Divisibilité dans Z.
Posté par matheux14
Bonsoir ,
Merci d'avance. 
1) Démontrer que 3 divise 5×4n-2 quel que soit l'entier naturel n.
2) Déterminer le reste de la division euclidienne de 20112012+20122011 par 13.
3) Démontrer à l'aide des congruences que pour tout entier naturel n , 3×52n+1 +23n+1 est divisible par 17.
4) Déterminer tous les entiers naturels n tels que 11 | 7×3n+3
bonsoir
1 : récurrence
ou bien
5
4n - 2 = 34n + 2(4n - 1)
et il suffit de savoir factorise (xn-1) par (x-1) ... ce qui a un rapport avec les suites géométriques
Bonsoir,
Pour le 1) essaye une démonstration par récurrence
Pour le 2) fais la remarque 20113 
1 [13] et 20126 1 [13]
Pour le 3) on peut le faire par récurrence
Pour le 4) ça marche pour n=2, n=7. Tu peux faire le conjecture n=5k + 2 et tu démontres par récurrence.
Ok ,
1) Soit An= 5×4n-2
P(n) : << 3| An >> quelque soit n de N.
* A0= 5×40-2
A0= 5-2
A0=3
Donc 3 | A0
* Soit k de N , supposons que 7 | Ak.
Ak+1= 5×4k+1 -2
Ak+1=5×4×4k-2
Ak+1=4×(5×4k-2)+4×2-2
Ak+1=4Ak+2(4-1)
Ak+1=4Ak+6
Comme 3 | Ak et 3 | 6 ,
3 | Ak+1.
Conclusion : Ak vraie ==> Ak+1 vraie.
Par conséquent , P(n) est vraie.
2)
Citation :
Pour le 2) fais la remarque 20113 1 [13] et 20126 1 [13]
Pour le 2) fais la remarque 20113
1 [13] et 20126 1 [13]Intéressant mais je n'arrive pas à le remarquer..
Bonjour,
Citation :
* Soit k de N , supposons que 7 | Ak.
* Soit k de N , supposons que 7 | Ak.
Ce n'est pas 7 qui divise Ak mais 3 (faute de frappe ?).
A part ça, c'est ok pour le 1)
Pour le 2), à quoi est congru 2011 modulo 13 ?
Puis 20112 ?
Puis 20113 ?
92 = 81 donc tu peux améliorer le résultat pour trouver un nombre < 13
Ensuite tu chercheras 20113 ??? [13] avec ??? toujours < 13
salut
matheux14 @ 14-12-2020 à 07:19
1) Soit An= 5×4n-2
P(n) : << 3| An >> quelque soit n de N.
faux ...1) Soit An= 5×4n-2
P(n) : << 3| An >> quelque soit n de N.
alma78 @ 14-12-2020 à 18:11
Exact.
Sachant que 2012=3*670+2 que peux-tu conclure sur 20112012 ??? [13] avec ??? toujours < 13
Exact.
Sachant que 2012=3*670+2 que peux-tu conclure sur 20112012
??? [13] avec ??? toujours < 13Je ne vois pas vraiment..
20112012 = 2011(3*670 + 2) = ( 20113)670 * 20112
Or 20113 1 [13] et 20112 3 [13]
D'où 20112012 ??? [13]
Bonjour , je ne comprends pas très bien ce que vous avez fait
alma78 @ 14-12-2020 à 19:24
20112012 = 2011(3*670 + 2) = ( 20113)670 * 20112
Or 20113 1 [13] et 20112 3 [13]
D'où 20112012 ??? [13]
20112012 = 2011(3*670 + 2) = ( 20113)670 * 20112
Or 20113
1 [13] et 20112 3 [13]
D'où 20112012
??? [13]Bonjour,
J'ai voulu utiliser le fait que 20113 1 [13]
J'ai donc décomposé 2012 en 3*670+2 d'où 20112012 = 20113*670+2
Qui s'ecrit aussi (20113)670 * 20112
Puis j'applique les règles sur les congruences.
Comme 20113 1 [13], on a (20113)670 1670 [13] or 1670=1 donc 20113*670 1 [13]
De plus 20112 3 [13]
Donc au final 201120121*3 [13] c'est à dire 3 [13]
Est ce que c'est plus clair ?
Il faut appliquer le même principe.
Mais ici il faut démontrer 20126 1 [13]
Et remarquer que 2011 = 6*335+1
Que trouves-tu ?
20122011=20126×335+1
=20126×335×2012
On a : 2012 ≡ 10[13] et 20126 ≡ 1[13] ==> 2012 6×335= ((20126))335 ≡ 1335[13] ≡ 1[13]
Donc 2012 2011 ≡ 10×1[13] ≡ 10[13].
2012 2011 ≡ 10[13].
C'est ça. On peut donc dire que 20112012 + 20122011 est divisible par 13.
Maintenant exercice 3) si tu en a toujours envie.
Par définition de la division euclidienne
a = b*q + r alors a r [b]
r, le reste de la division de a par b est inférieur strict à b
Donc si a b [b] ça s'écrit a = b*q + b = b*(q+1) + 0
Le reste de la division de a par b est donc ici 0.
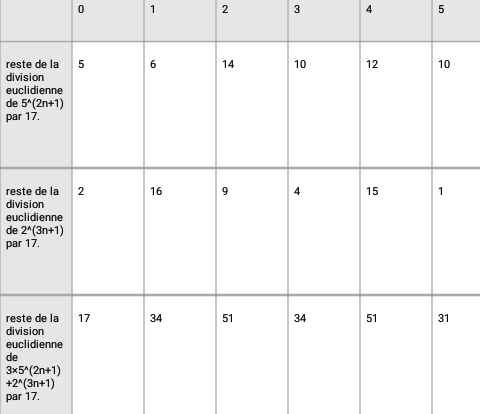
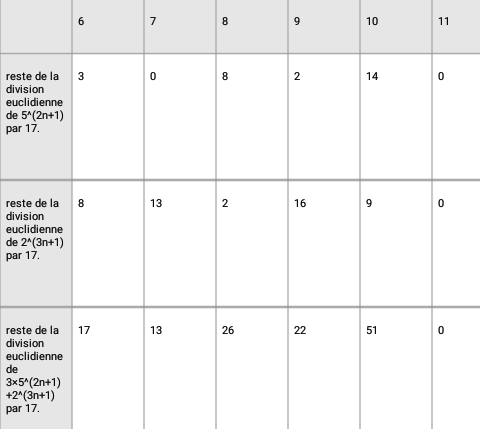
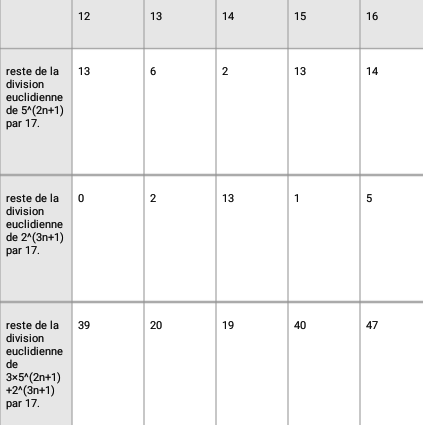
Vu qu'on s'intéresse à [17], le tableau risque d'être long à faire. Mais essaye quand même.
Après, je te montrerais une solution plus rapide. Mais, ça se mérite ... 
matheux14 @ 18-12-2020 à 19:16
Oui mais je ne comprends pas pourquoi si a ≡ b [b] alors a ≡ 0 [b]
Oui mais je ne comprends pas pourquoi si a ≡ b [b] alors a ≡ 0 [b]
alma78 @ 18-12-2020 à 19:34
Par définition de la division euclidienne....
ce n'est pas tant un pb de division euclidienne c'est simplement la définition de l'écriture Par définition de la division euclidienne....
si b = n alors a - b est multiple de b
donc par définition de "être multiple de" il existe un entier k tel que a - b = kb <=> a = (k + 1)b <=>(1) a est multiple de b <=>(2) a - 0 est multiple de b <=>(3) a
0 [b]
(1) et (3) : par définition
(2) : car trivialement a = a - 0
juste en passant pour montrer que ce n'est pas la division euclidienne qui justifie le résultat mais les définitions élémentaires de base de l'arithmétique
Bonjour,
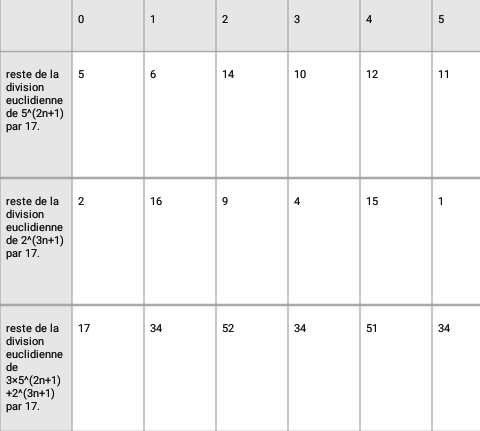
En bas de ton tableau tu dois avoir un reste égal à 0.
Lorsque tu trouves 17, 34, 51, ces nombres sont congrus à 0 modulo 17 . Dans ce cas, c'est bon. Mais lorsque tu trouves 31, 13, ce n'est pas bon. Donc refais tes calculs lorsque tu trouves en bas de colonne un nombre qui n'est pas multiple de 17.
Exemple d'erreur : pour n=5, 5(2*5+1)=51111 [17]. Toi, tu trouves 10, ce qui est faux.
Bonjour,
Tu n'oubliera pas de compléter ton tableau jusqu'à n = 16.
Pour l'autre technique :
Je vais poser A = 3*5(2n+1) + 2(3n+1) pour éviter de retaper la formule à chaque fois
A = 3*52n*5 + 23n*2
A = 3*5*(52)n + 2*(23)n
A = 15*25n + 2*8n
On a 258 [17] donc 25n8n [17]
D'où A 15*8n + 2*8n [17]
A(15 + 2)*8n [17]
A17*8n [17]
Ce qui signifie que A est divisible par 17.
Voilà !
Citation :
Pour le 4) ça marche pour n=2, n=7. Tu peux faire le conjecture n=5k + 2 et tu démontres par récurrence.
Pour le 4) ça marche pour n=2, n=7. Tu peux faire le conjecture n=5k + 2 et tu démontres par récurrence.
Comment et pourquoi conjecturer n=5k+2 ?
Parce que tu va montrer que c'est divisible par 11 pour n=2, puis n=7. Donc a priori à chaque fois que n augmente de 5 avec un premier cas pour n=2. Donc n pourrait être de la forme 2 + 5k (c'est ce que tu peux conjecturer). Ensuite tu vas le démontrer par récurrence . Tu as déjà vérifié le cas k=0 (n=2).