Inscription / Connexion Nouveau Sujet
DL avec cotan en 0
Bonjour,
Je dois étudier le fonction en 0.
J'ai un équivalent en 0 qui est 1^(1/x) donc forme indéterminée.
Pour le DL, j'en suis à .
Je ne sais plus vraiement quoi faire... Un peu d'aide ne serait pas de refus!
Merci d'avance
Bonjour
Prends le logarithme...
C'est vrai que c'est horrible d'écrire que c'est équivalent à mais tu es bien dans un cas d'indétermination.
Merci de vos réponses ; j'ai un équivalent avec le logarithme qui est -4x/3mais après il faut que je repasse à l'exponentielle, ce qui n'est pas possible avec les équivalents me semble t-il...
En prenant le logarithme sur le DL j'ai toujours la cotan qui m'ennui...
Je suis d'accord. Mais après pour avoir la tangeante et la position par rapport à celle-ci? Il ne faut pas faire le DL?
Juste une petite mise au point : "étudier" la fonction, ça veut dire trouver la limite, la dérivée, et la position par rapport à le tangeante, non?
Je trouve 1 par valeurs inférieures. Mais je ne sais pas si j'ai le droit de dire qu'en 0, ln(f) est équivalent à -4x/3, donc qu'en 0+, ln(f) vaut 0- et finalement que f tend vers 1-...
f(x) = (2.x.cotg(2x))^cotg(x)
Près de 0 : cotg(2x) = 1/(2x) - 2x/3 et cotg(x) = 1/x
f(x) = (1 - 4x²/3)^(1/x) (Aux alentours de 0, 0 exclu)
---
ln(f(x)) = ln(1 - 4x²/3)/x
lim(x--> 0) [ln(1 - 4x²/3)/x] est de la forme 0/0 ---> règle de Lhospital.
= lim(x--> 0) [(-8x/(1 - 4x²/3))/1] = 0
et donc lim(x --> 0) f(x) = 1
On peut prolonger f(x) en 0 par f(0) = 1
----
On a donc :
f(x) = (1 - 4x²/3)^(1/x) (Aux alentours de 0, 0 exclu)
f(0) = 1 (si on prolonge en 0)
-----
Sauf distraction. 
Oui camellia j'avais aussi vérifié sur le graphique, merci.
Et JP, je pense que je vais m'en tenir à mes équivalents parce que Lhospital.. Connais pas!
Maintenant, la partie où je n'ai vraiment pas d'idée : la dérivée et la tangente?.. Comme je l'ai dit j'étais parti sur un DL mais je bloque avec la puissance cotan... (4e ligne de mon premier post).
Si c'est bien aux alentours de 0 que tu veux travailler.
Si tu veux avoir la tangente en 0, il faut commencer par prolonger la fonction en 0 (par f(0) = 1)
Et près de 0, les DL amènent : f(x) = (1 - 4x²/3)^(1/x) à prolonger par f(0) = 1
f'(0) = lim(x--> 0) [(f(x) - f(0))/x] = lim(x--> 0) [(f(x) - 1)/x] = -4/3 (qu'il te faudra trouver avec tes armes).
T0 : y = (-4/3).x + 1 (Equation de la tangente en 0)
-----
Sauf distraction. 

 x
x  0
0 
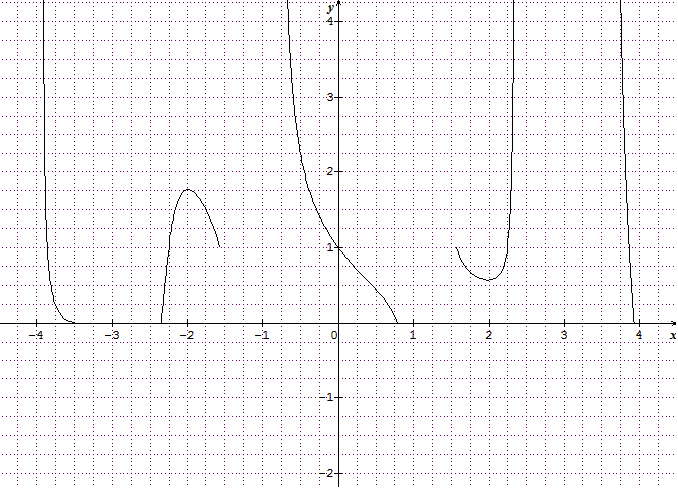

 analyse en post-bac
analyse en post-bac