Inscription / Connexion Nouveau Sujet
DM: fonction
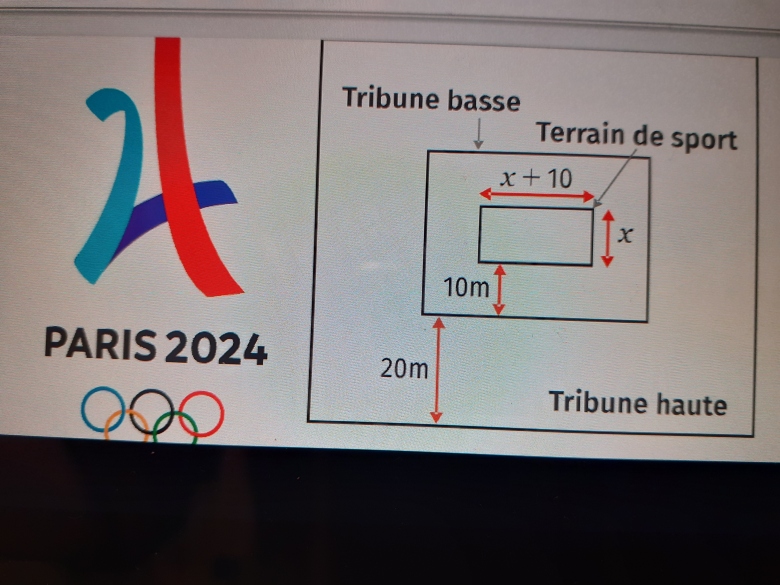
Pour les jeux olympiques a Paris, on envisage de construire une salle multisport suivant les contraintes indiquées ci-dessus ( avec x compris entre 10 et 50 mètre)
1. Determiner l'aire Ts du terrain de sport en fonction de x.
Aire Ts:
x^2+10x
2. On note Tb. L'aire au sol de la tribune basse.
Démontrer que, pour tout x appartient [10;50].
Tb(x)= (x+20)(x+30)-Ts(x) puis simplifier l'expression de Th
Tb(x)= 40x+600
Pour simplifier je suis pas sure je factorise d'où
40x+40×15
40(x+15)
Pour démontrer je sais pas
3. On note Th , l'aire au sol de la tribune haute
Démontrer que, pour tout x appartient [10;50].
Th(x)=(x+60)(x+70)-(x+20)(x+30) puis simplifier l'expression de Th
Th(x)=80x+3600
Je suis toujours pas sur si pour simplifier il faut factoriser
80x+3600
80x+(80×45)
80(x+45)
Je sais pas comment démontrer pour cette question aussi
Merci pour votre avance
Merci
Bonsoir
L'aire de la tribune basse c'est l'aire du rectangle moyen moins l'aire du petit rectangle qui correspond au terrain
pareil pour l'aire de la grande tribune : l'aire du grand rectangle moins l'aire du rectangle moyen (qui correspond à tribune basse + terrain)
Aucunes erreurs, mais tu as réussi a démontrer les expressions de Tb et Th grâce au post de zormuche?
Je pense mais je suis pas sure encore , il faut bien démontrer par un petit paragraphe ou un schéma ?
Un schéma propre et clair (avec par exemple des aires hachurés) pour Tb et aussi un autre pour Th devrait suffire
4. Le coût de construction du mètre carré en tribune basse est trois fois plus élevé qu'en tribune haute.
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions TBet 3×TH
Sachant que TB(x)= 40x+600 et TH(x)=80x+3600
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse coûtera moins cher que la tribune haute.
(On pourra noter c le coût de construction au mètre carré de la tribune haute.)
5. Pendant les jeux olympiques , le prix des places au mètre carré en tribune haute est quatre fois moins important qu'en tribune basse.
a. Représenter, à l'aide de Geogebra les fonctions de TB et 1/4×TH.
b. Determiner graphiquement puis algebriquement les valeurs de x pour lesquelles la tribune basse engendrera plus de recettes que la tribune haute. (On note p le prix au mètre carré des places de la tribune basse)
J'ai des idées mais je suis pas sure et je ne sais pas utiliser Geogebra
Merci de votre aide
*** message déplacé ***
*** message déplacé ***

Par ailleurs, un exo qui commence par la question 4, c'est pas banal.
*** message déplacé ***
*** message déplacé ***
... Double post ![]() DM: fonction
DM: fonction
*** message déplacé ***
*** message déplacé ***
Le premier dm fonction c'est le mien et ces le reste des questions de mon dm
*** message déplacé ***
*** message déplacé ***
Autrement dit, c'est le même exo : il doit être dans le même sujet.
J'ai des idées mais je suis pas sure
*** message déplacé ***
*** message déplacé ***
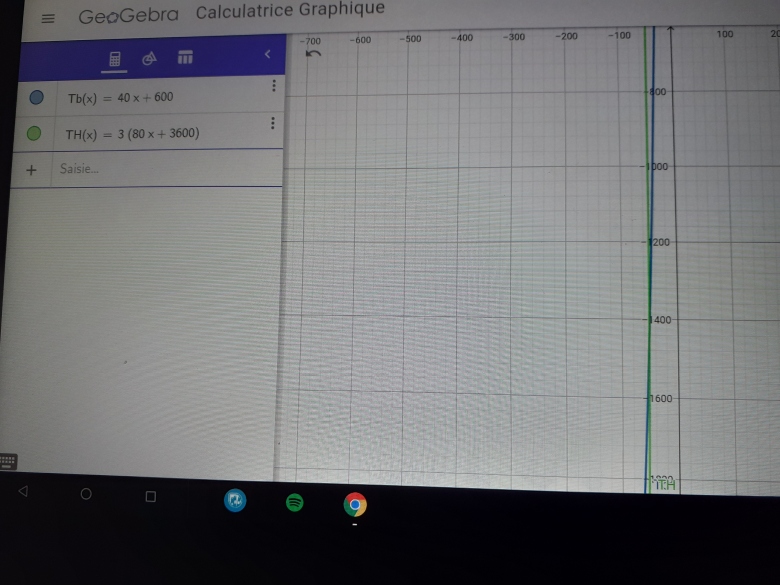
J'ai tracer les deux fonctions mais je ne trouve pas l'interprétation
*** message déplacé ***
*** message déplacé ***
Change les échelles de tes axes, cette figure est illisible.
mais je ne trouve pas l'interprétation
*** message déplacé ***
*** message déplacé ***
Comprends-tu que c'est infaisable sans avoir le début de l'exo ?! ...
On va donc attendre qu'un modérateur déplace cette partie.
*** message déplacé ***
*** message déplacé ***
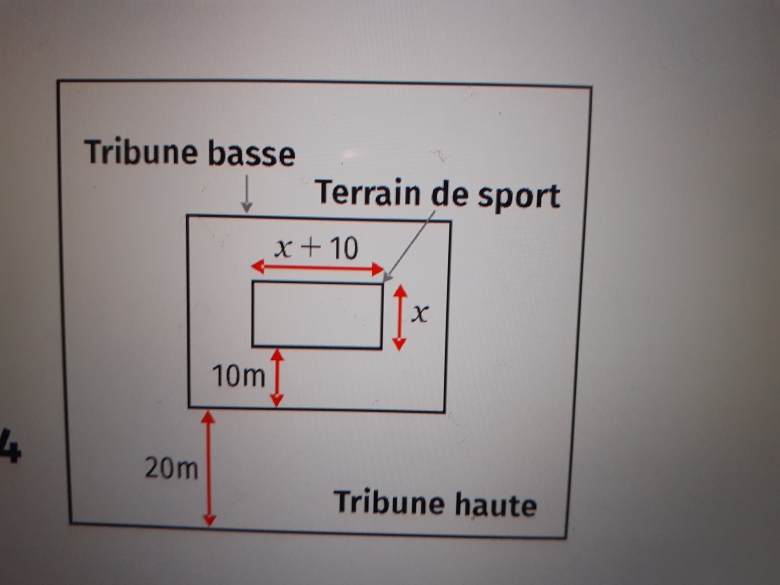
Pour les jeux olympiques a Paris, on envisage de construire une salle multisport suivant les contraintes indiquées ci-dessus ( avec x compris entre 10 et 50 mètre)
1. Determiner l'aire Ts du terrain de sport en fonction de x.
Aire Ts:
x^2+10x
2. On note Tb. L'aire au sol de la tribune basse.
Démontrer que, pour tout x appartient [10;50].
Tb(x)= (x+20)(x+30)-Ts(x) puis simplifier l'expression de Th
Tb(x)= 40x+600
Pour simplifier je suis pas sure je factorise d'où
40x+40×15
40(x+15)
Pour démontrer je sais pas
3. On note Th , l'aire au sol de la tribune haute
Démontrer que, pour tout x appartient [10;50].
Th(x)=(x+60)(x+70)-(x+20)(x+30) puis simplifier l'expression de Th
Th(x)=80x+3600
Je suis toujours pas sur si pour simplifier il faut factoriser
80x+3600
80x+(80×45)
80(x+45)
4. Le coût de construction du mètre carré en tribune basse est trois fois plus élevé qu'en tribune haute.
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions TBet 3×TH
Sachant que TB(x)= 40x+600 et TH(x)=80x+3600
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse coûtera moins cher que la tribune haute.
(On pourra noter c le coût de construction au mètre carré de la tribune haute.)
5. Pendant les jeux olympiques , le prix des places au mètre carré en tribune haute est quatre fois moins important qu'en tribune basse.
a. Représenter, à l'aide de Geogebra les fonctions de TB et 1/4×TH.
b. Determiner graphiquement puis algebriquement les valeurs de x pour lesquelles la tribune basse engendrera plus de recettes que la tribune haute. (On note p le prix au mètre carré des places de la tribune basse)
*** message déplacé ***
Regarde j'ai tout regroupé dans un autre post DM: fonction exercice complet
Tu peux aller voir stp
*** message déplacé ***
*** message déplacé ***
Ce que tu as fait est interdit !
Tuas ton exo sur trois sujets maintenant.
Bref, on attend qu'un modérateur vienne faire le ménage 
*** message déplacé ***
*** message déplacé ***


