Inscription / Connexion Nouveau Sujet
Dm Lecture graphique- Tracé une courbe
bonjour,
Le plan est muni d'un repère orthonormal (o;i;j)
On a représenté en annexe la courbe T de la fonction f définie sur R par f(x)=ax²+bx+c où a,b et c dont des réels donnés, a0.
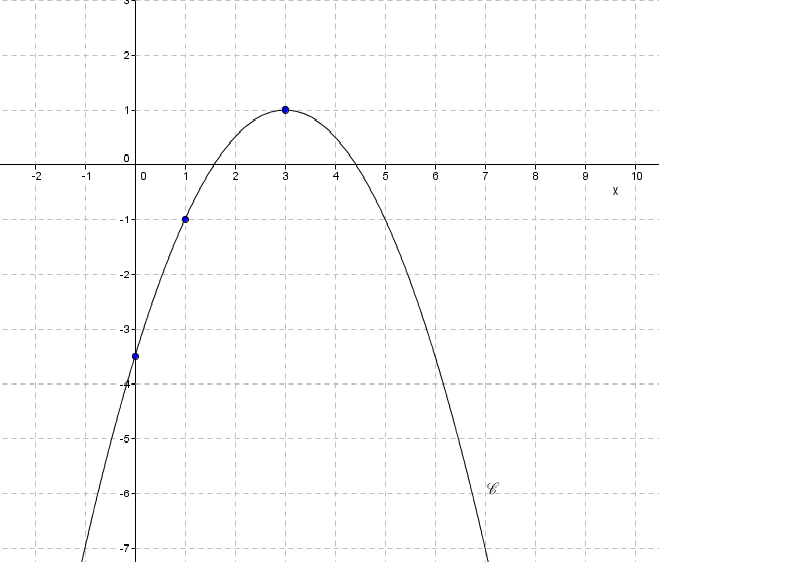
On a placé les point de T suivants A(0;-3.5),B(1;-1)et s(3;1).
Partie A Lecture graphique- Tracé une courbe
1.a) En utilisant le point A, déterminer la valeur de c.
b)En utilisant les points B et S donner les valeurs de f(1) et f(3)
En déduire que les nombres a et b sont solutions du système
c) Résoudre ce systeme et déterminer l'éxpression de f(x).
d) que peut-on dire du point S
2.On considère la fonction de g définie sur R par g(x)=(x-3)(x-7)et on désigne par T' sa représentation graphique dans le repère (o;i;j).
a)Déterminer la nature de la courbe T' et préciser ses éléments caractéristiques.
b) Construire avec soin la courbe T' sur l'annexe.
3.a) Résoudre l'équation g(x)=0
b) Conjecturer le nombre de solution de l'équation f(x)=0
Donner un encadrement de chacune d'elle par des entiers.
Voici l'annexe:
Bonjour, et alors tu en es où ?
toute la partie A utilise le fait que si un point est sur une courbe alors ses coordonnées satisfont l'équation de la courbe, il n'y a pas grandes difficultés.
En utilisant le point A, déterminer la valeur de c.
C'est tout simple, A(0;-3.5) est sur la courbe donc les coordonnées de A satisfont l'équation y=ax²+bx+c
ça donne immédiatement c=-3.5 si on remplace x par 0
d'accccooord j'ai compris effectivement vu comme sa c'est moins compliqué
pour la question b quant-il disent f(1) et f(3) quest ce que c'est ? c'est leur coordonnées?
B(1;-1)et S(3;1) et on sait que ces points sont sur la courbe donc f(1) c'est l'ordonnée de B et f(3) l'ordonnée de S, donc ....
les maths et moi c'est une longue histoire d'incompréhension :p C'est assez incompréhensible ce que tu écris 
-1+1=2.5 
C'est a+b=2.5 ; 3a+b=1.5 que tu essayes de résoudre ?
Et bien tu prends a dans l'une et tu remplaces dans l'autre (ou encore tu les soustrais membre à membre pour te débarrasser de b).
donc si je soustrais membre a membre j'ai si onremplace a et b : -1+1=2.5
3*-1+1=1.5
donc 0=2.5
-2=1.5
c'est sa ?
Toujours aussi incompréhensible 
. Et pourquoi veux-tu remplacer a et b par quelque chose ? a et b c'est ce qu'on cherche.
3a + b = 1.5
a + b = 2.5
tu les soustrais membre à membre, ça donne quoi ?
3a-a = 1.5 - 2.5 
2a = -1 
a=-1/2
et b=2.5-a=5/2+1/2=3
Donc normalement on a trouvé que la parabole avait pour équation y=-x²/2+3x-3.5
Et il est toujours bon de vérifier, c.a.d dessiner les 3 points et la courbe pour vérifier qu'ils sont bien dessus :
ça a l'air de bien coller 
ha non aucun rapport. f(1) c'est quand on fait x=1 dans ax²+bx+c donc f(1)=a+b+c et f(3)=9a+3b+c
(on se demande comment tu es arrivé à trouver le système de la question 1b ? )
non, je t'ai aidé à résoudre le système. Mais je n'ai pas vu comment tu as établis qu'il fallait que a+b=2.5 et 3a+b=1.5 ?
non, tu n'as pas compris ma question. Ça c'est pour résoudre, mais pourquoi faut-il que a+b=2.5 et 3a+b=1.5 ?, tu l'as démontré ? C'était la question 1b)
je ne comprends pas ce que tu dis.
on t'a demandé de démontrer qu'il fallait que a+b=2.5 et 3a+b=1.5 . L'as-tu fait ? Et comment ?
Essaye de le dire clairement. Si tu écris sur une copie ce que tu dis dans tes posts, tu auras 0 à la question.
mais dans la question 1b il ne demande pas de démontrer il demande de donner les valeurs
b)En utilisant les points B et S donner les valeurs de f(1) et f(3)
je parlais de la suite de la question :
En déduire que les nombres a et b sont solutions du système a+b=2.5 et 3a+b=1.5
ah désoler bah je ne l'ai pas faite mais je suppose que l'on doit prouver en calculant pour affirmer la question
on suppose que a et b sont solution du système on le prouve par le calcul suivant
juste pour savoir si je met sa pour le calcul est-ce bon?
a+b=2.5 3a+b=1.5
b=-a+2.5 -3a+(-a)+2.5=1.5
b=a+2.5 2a+2.5=1.5
b=a+2.5 2a=2.5-1.5
b=a+2.5 2a=1
b=1+2.5 2a=1
b=3.5 a=0.5
non, il y a des fautes, voir démonstration dans mon post du 10-05-14 à 14:4 (je ne vais pas te la refaire plein de fois non plus)
et puis ça c'est la résolution du système, ça n'est pas établir que le système est a+b=2.5 ; 3a+b=1.5 , mais bon je te l'ai déjà dit 4 fois, je ne vais pas continuer, je vois que ça ne sert à rien 
.
bah on déduit par le calcul du système qui a était fait par toi je voit pas comment prouverj'ai fait le devoir est-ce possible de me dire si oui ou non c'est juste merci
1.a) a(0;-3.5)
f(0)=-3.5 et ax²+bx+c=-3.5
f(0)=0+0+c=-3.5
c=-3.5
b(1;-1) et s(3;1)
f(1)= a (1)²+b(1)+c=-1
a+b=2.5
f(3)= a(3)²+b(3)+c=1
9a+3b-3.5=1
9a+3b=4.5 3a+b=1.5
b) (1)a+b=2.5
(2)3a+b=1.5
(1)b=2.5-a
(2)3a+(2.5-a)=1.5 2a=-2.5+1.5
2a=-1
a=-0.5
b=2.5-a
b=2.5+0.5
b=3
donc f(x)= -0.5x²+3x-3.5
d)Le point s est le sommer de la parabole
2.a) La courbe C est une parabole sont sommet est (5;4)
Oui c'est bien.
Pour d) tu affirmes, mais tu pourrais aussi le démontrer que S est le sommet (qui s'écrit avec un t à la fin) ?
2.a) l'abscisse du sommet est bien 5, mais l'ordonnée c'est -4 et pas +4
Annuler
connectez vous