Inscription / Connexion Nouveau Sujet
Dm maths
Bonjour je ne comprend pas l'exercice . Je suis arrivé à la question b) ensuite je suis bloqué .
: Avec des petits carrés identiques, disposés comme le montrent les figures ci-dessous, on constitue un nouveau carré.
Exercice n°1: Avec des petits carrés identiques, disposés comme le montrent les figures ci-dessous, on constitue un nouveau carré.
a. Réalise une figure avec quatre petits carrés sur un côté. Indique le nombre total de carrés coloriés. Recommence avec une figure de six petits carrés de côté. S'il y a 100 petits carrés sur le côté, combien y-a-t-il de carrés coloriés au total ?
b. On appelle n le nombre de petits carrés d'un côté. On veut obtenir une formule en fonction de n qui donne le nombre total de carrés coloriés dans le nouveau carré.
• Chloé dit: «Je pense que la
Sofiane lui répond alors : « Mais non ! Tu Justifie la réponse de Sofiane et établis une première formule.
• Sur les cahiers de trois élèves, on observe les schémas suivants :
DEVOIR NON SURVEILLE DE MATHEMATIQUES N°4
Exercice n°1: Avec des petits carrés identiques, disposés comme le montrent les figures ci-dessous, on constitue un nouveau carré.
a. Réalise une figure avec quatre petits carrés sur un côté. Indique le nombre total de carrés coloriés. Recommence avec une figure de six petits carrés de côté. S'il y a 100 petits carrés sur le côté, combien y-a-t-il de carrés coloriés au total ?
b. On appelle n le nombre de petits carrés d'un côté. On veut obtenir une formule en fonction de n qui donne le nombre total de carrés coloriés dans le nouveau carré.
• Chloé dit: «Je pense que la
Sofiane lui répond alors : « Mais non ! Tu Justifie la réponse de Sofiane et établis une première formule.
• Sur les cahiers de trois élèves, on observe les schémas suivants :
En suivant les découpages de Jean et de Fatima, établis deux nouvelles formules.
À l'aide de son schéma, Bakari remarque que le nombre de carrés coloriés est un multiple de 4. Justifie sa remarque et déduis-en une quatrième formule.
En utilisant chacune de ces quatre formules, calcule le nombre total de carrés coloriés lorsqu'il y en a 15 sur un côté. Les résultats trouvés étaient-ils prévisibles ?
b. Développe et réduis chacune des trois dernières formules en utilisant la propriété de distributivité. Qu'as-tu démontré ?
c. L'unité d'aire est la surface d'un des petits carrés coloriés utilisés pour constituer le nouveau carré.
• En considérant des aires, établis une cinquième formule donnant le nombre total de carrés coloriés en
fonction de n.
• Utilise cette nouvelle formule pour calculer le nombre total de carrés pour n = 4 ; n = 6 ; n = 15 et
n = 100. Les résultats obtenus sont-ils cohérents ? Pourquoi ?
En utilisant les résultats des questions précédentes, démontre que (n - 2)2 = n2 - 4n + 4.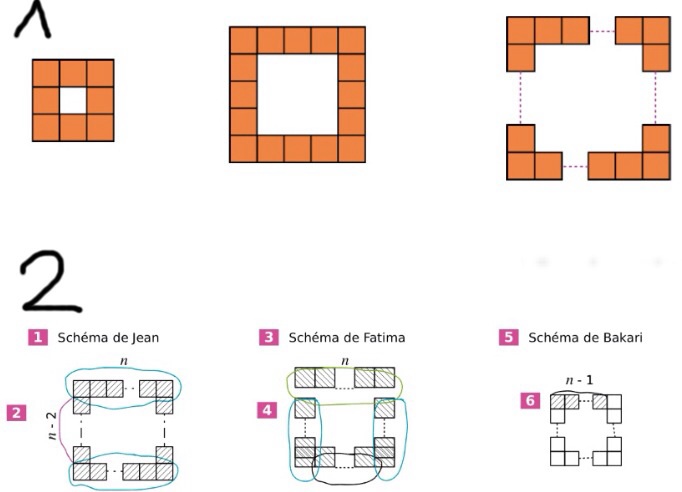
bonjour,
a. Réalise une figure avec quatre petits carrés sur un côté.Indique le nombre total de carrés coloriés.
-->12
Recommence avec une figure de six petits carrés de côté.--->20
S'il y a 100 petits carrés sur le côté, combien y-a-t-il de carrés coloriés au total ? -->100+100+98*2=396
b. On appelle n le nombre de petits carrés d'un côté. On veut obtenir une formule en fonction de n qui donne le nombre total de carrés coloriés dans le nouveau carré.
• Chloé dit: «Je pense que la ..................Sofiane lui répond alors : « Mais non ! Tu Justifie la réponse de Sofiane et établis une première formule. .???????????
il doit manquer quelque chose!!!
il y deux lignes horizontales parallèles de 100 et 2 lignes verticales parallèles de 98 : on ne compte pas 2 fois les carrés des coins
Bnjour,
Oui je suis desolé .
Chloé dit :"Je pense que la formule est 4n ".
Merci mais je suis bloqué aprés la question b) . Pourriez-vous m'aidez ?
d'après jean : 2n+2(n-2)=4n-4=2(2n-2) nb pair
d'après fatima : n+n-2+2(n-1)=4n-4
d'après Bakari : 4(n-1)=4n-4
avec les aires :
avec 3 carrés de côté, n=8-->3*3-1=8=3²-1²=3²-(3-2)²=n
avec 5 carrés de côtés, n=16-->5*5-3*3=5²-(5-2)²=16=n
avec 100 carrés de côtés, n=396-->100²-98²=100²-(100-2)²=396=n
formule :nb de carrés=n²-(n-2)²=n²-(n²-2n+4)=n²-n²+2n-4=2n-4
Bonjour, alors voila mon exercice, j'ai reussi jusqu'a la question b) ensuite je suis bloqué ! Merci de bien vouloir m'aider.
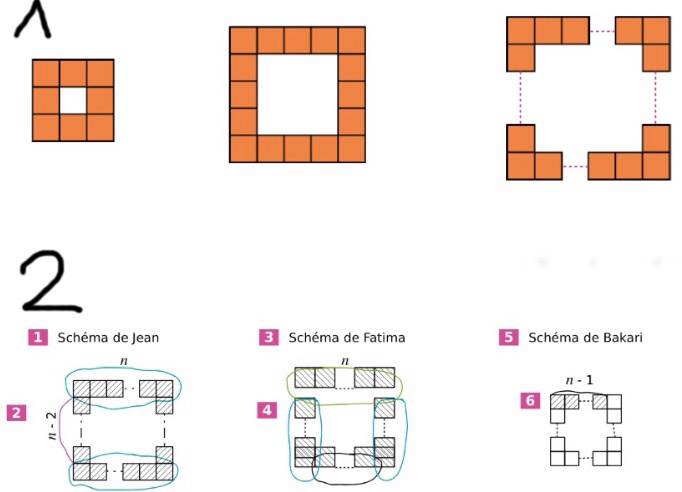
:Exercice n°1 Avec des petits carrés identiques, disposés comme le montrent les figures ci-dessous, on constitue un nouveau carré.
Schéma 1 ...
a. Réalise une figure avec quatre petits carrés sur un côté. Indique le nombre total de carrés coloriés. Recommence avec une figure de six petits carrés de côté. S'il y a 100 petits carrés sur le côté, combien y-a-t-il de carrés coloriés au total ?
b. On appelle n le nombre de petits carrés d'un côté. On veut obtenir une formule en fonction de n qui donne le nombre total de carrés coloriés dans le nouveau carré.
• Chloé dit: «Je pense que la formule est 4n
Sofiane lui répond alors : « Mais non tu en as trop!
Tu Justifie la réponse de Sofiane et établis une première formule.
• Sur les cahiers de trois élèves, on observe les schémas suivants :
Schéma 2 ...
En suivant les découpages de Jean et de Fatima, établis deux nouvelles formules.
À l'aide de son schéma, Bakari remarque que le nombre de carrés coloriés est un multiple de 4. Justifie sa remarque et déduis-en une quatrième formule.
En utilisant chacune de ces quatre formules, calcule le nombre total de carrés coloriés lorsqu'il y en a 15 sur un côté. Les résultats trouvés étaient-ils prévisibles ?
b. Développe et réduis chacune des trois dernières formules en utilisant la propriété de distributivité. Qu'as-tu démontré ?
c. L'unité d'aire est la surface d'un des petits carrés coloriés utilisés pour constituer le nouveau carré.
• En considérant des aires, établis une cinquième formule donnant le nombre total de carrés coloriés en
fonction de n.
• Utilise cette nouvelle formule pour calculer le nombre total de carrés pour n = 4 ; n = 6 ; n = 15 et
n = 100. Les résultats obtenus sont-ils cohérents ? Pourquoi ?
En utilisant les résultats des questions précédentes, démontre que (n - 2)2 = n2 - 4n + 4.
*** message déplacé ***
bonjour,
cet exo est passé hier, regarde ![]() Dm maths
Dm maths
*** message déplacé ***


