Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde FonctionsTopics traitant de fonctions [tout]Lister tous les topics de mathématiques
Niveau seconde
Partager :

DM : optimisation de boîte de conserve

Posté par
Nicole974 21-01-16 à 14:36

Bonjour à tous, j'ai un DM à faire mais je n'y comprends rien . Dans ce DM il existe 2 partie , j'ai réussi à répondre à la première mais la deuxième est assez complexe . J'aimerais bien avoir votre aide s'il-vous-plaît. Voici le sujet :

Dans le commerce, les boîtes de conserve cylindrique de même contenance ont toutes les mêmes dimensions.Comment ces dimensions ont-elles été choisies ?

Partie A: un peu de calcul littéral ( Mes réponses sont situées juste après l'énoncer)
On considère une boîte de conserve de hauteur h et de rayon r.
1) Exprimer le volume V d'un cylindre de hauteur h et dont le rayon de la base est r .  
V=( X R[/sup]) X h
2) En déduire une expression de h en fonction de V et de r . h=V/( X r[sup])
3) Exprimer l'aire A de ce cylindre en fonction de h et de r . A=2 X X r X h + 2 X X r[/sup]
4) En remplaçant h par l'expression trouvée précédemment, exprimer A en fonction de V et r . A=2 X (V/ X r[sup])
  
Partie B : du concret
Dans le commerce , on trouve des boîtes de conserve de 212cm3 , 425cm3 , 850cm3.
1)Donner l'expression des trois fonctions qui , au rayon de la base de la boîte de conserve, associent l'aire de la boîte pour les trois volumes proposés.
Les nommer A212 , A425, A850.
2) Utiliser la calculatrice ou un tableur pour tracer dans un même repère ces trois fonctions.
3) Déterminer le minimum pour chacune des trois fonctions au dixième près. ( si besoin dresser un tableau de valeur pertinent).
4)En reprenant l'expression de  h en fonction de r et V de la partie A , calculer la hauteur correspondante pour chacun des trois volumes étudiés et des trois rayons déterminés.
5) À votre avis, quels objectifs ont sous-tendu le choix des dimensions des boîtes de conserve cylindrique?

Je vous remercie d'avance pour votre aide .

Posté par
Glapion Moderateurre : DM : optimisation de boîte de conserve 21-01-16 à 14:51

Bonjour, tu devrais t'inspirer de ce topic là : DM optimisation de boîtes de conserve

Posté par
heklare : DM : optimisation de boîte de conserve 21-01-16 à 14:54

Bonjour
la partie B est l'application de la partie A
pour l'aire de la boîte vous avez dû trouver

\mathcal{A}=2\times \pi R^2+2 \pi R \dfrac{v}{\pi R^2}
soit après simplification
\mathcal{A}=2\times \pi R^2+ \dfrac{2v}{R}
il suffit de remplacer dans la première question v par la donnée du volume

Posté par
Nicole974Aire d'un cylindre 24-01-16 à 16:09

Peut-on avoir deux façons de calculer l'aire d'un cylindre ? Si oui pourriez-vous m'expliquez ?

*** message déplacé ***

Posté par
Nicole974re : DM : optimisation de boîte de conserve 24-01-16 à 16:19

Merci , mais pourquoi a-t-on de façon de calculer l'aire ?

Posté par
Glapion Moderateurre : Aire d'un cylindre 24-01-16 à 16:29

inutile de créer un topic pour ça. Reste sur ton topic existant !

*** message déplacé ***

Posté par
heklare : DM : optimisation de boîte de conserve 24-01-16 à 16:32

Pour pouvoir fabriquer une boîte, on construit un patron. Savoir de quelle surface, on va avoir besoin pour construire la boîte. L'intérêt est donc de trouver l'aire du cylindre qui demandera le moins de métal possible tout en respectant certaines contraintes

Posté par
heklare : DM : optimisation de boîte de conserve 24-01-16 à 16:34

Il n'y a qu'une manière de calculer l'aire d'un cylindre

Posté par
Nicole974re : DM : optimisation de boîte de conserve 24-01-16 à 16:58

Je viens de comprendre une des erreurs que j'ai fais en revoyant les expressions . Mais sachant qu'en calculant l'aire d'une cylindre Partie A énoncer 3 , pourquoi l'un des rayons n'est pas au carré ?

Posté par
heklare : DM : optimisation de boîte de conserve 24-01-16 à 17:06

Certainement dû à une simplification

la surface du  cylindre se compose d'un rectangle et de deux disques
l'aire d'un disque  \pi R^2

l'aire du rectangle   2\pi R \times h =2\pi R\times \dfrac{v}{\pi R^2}=\dfrac{2\pi R \times v}{\pi R^2}=\dfrac{2v}{R}

Posté par
Nicole974re : DM : optimisation de boîte de conserve 25-01-16 à 09:03

merci , et donc faut-il mettre  cette expression sur la calculatrice pour pouvoir avoir le graphique  : 2 x x r x (212/ x r2 , svp ?

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 10:23

pour la première boîte
2 \pi x^2+\dfrac{424}{x}

pour la deuxième
2\pi x^2+\dfrac{2\times 425}{x}

les calculatrices n'acceptant pas d'autres inconnues que x

Posté par
Nicole974re : DM : optimisation de boîte de conserve 25-01-16 à 10:59

Est-ce normale que ma calculatrice affiche des droites constantes mais verticale ?
J'ai oublier  une phrase dans l'énoncer 3 de la partie B qui est : "Relever leur antécédent et les nommer r212 , r425 , r850 ".  Leur antécédent est donc 0 .

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 11:40

Non il faudrait changer les valeurs de la fenêtre
x 0 10
y  0 1000
scale y 10

pour les deux premières j'obtiens 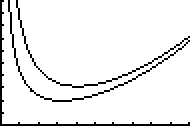DM : optimisation de boîte de conserve

utilisez trace pour lire les minima

Posté par
Nicole974re : DM : optimisation de boîte de conserve 25-01-16 à 11:50

Le problème c'est que j'ai une calculatrice  TI-82 Advanced Texas instrument .
Donc j'ai cela :
Xmin=  -10
Xmax=   10
Xgrad= 1
Ymin=  -10
Ymax= 10
Ygrad=  1
Xres=  1

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 12:02

les valeurs de la fenêtre se changent

Donc j'ai mis :
Xmin=  0
Xmax=   10
Xgrad= 1
Ymin=  0
Ymax= 1000
Ygrad=  10
Xres=  1

vous aurez les graphiques précédents

Posté par
Nicole974re : DM : optimisation de boîte de conserve 25-01-16 à 13:20

Donc les antécédents sont :
1er: 3,1
2ème : 4
3ème: 5,1
leur minimum :
r212= 196,8
r425=313
r850= 496,7
En conséquent leur hauteur sont :
1er : 7cm
2ème: 8cm
3ème : 10cm
Est-ce exacte svp ?

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 13:50

\begin{array}{|c|c|c|c|}\hline & \text{minimum}  &\text{valeur pour laquelle il est atteint}& \text{hauteur}\\\hline 1&196.8&3.2&6.6\\\hline2&313&4.07&8.5\\\hline3&496.8&5.1&10.4\\\hline \end{array}

Posté par
gsap9re : DM : optimisation de boîte de conserve 25-01-16 à 15:32

bonjour j'ai le même exercice et je voudrais savoir comment avez vous trouver la hauteur svp ?

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 15:35

Bonjour
c'était écrit dans le texte

puisque v=\pi R^2 h alors h=\dfrac{v}{\pi R^2}

Posté par
Nicole974re : DM : optimisation de boîte de conserve 25-01-16 à 15:41

Merci infiniment hekla pour votre aide !!

Posté par
heklare : DM : optimisation de boîte de conserve 25-01-16 à 16:04

de rien

Posté par
LeDinore : DM : optimisation de boîte de conserve 25-01-16 à 18:30

Bonjour,

Voici un petit résultat qui dépasse le programme de seconde mais qui permet de recouper l'exercice...
Une boîte de conserve "optimale" a une hauteur égale à son diamètre.

La preuve :

V = \pi r^2 h
A = 2 \pi r h + 2 \pi r^2 = \dfrac{2V}{r} + 2\pi r^2

On se place à volume constant, et on cherche le rayon qui minimise l'aire A.

\dfrac{dA}{dr} = A' = -\dfrac{2V}{r^2} + 4\pi r = -\dfrac{2\pi r^2 h}{r^2} + 4\pi r = -2\pi h} + 4\pi r = 0  \implies \boxed{  h = 2r = \sqrt[3]{\dfrac{4V}{\pi}} }

Pour   V = 850   /   425   /   212    on trouve    h  =  10.27   /   8.15   /   6.46
... et le rayon qui vaut la moitié...


Rechercher
Menu
Espace membre
8 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !