Inscription / Connexion Nouveau Sujet
dm sur les radians
bonjour
j'aurai aimé savoir si quelqu'un peut m'aider pour cette exercice que j'ai a faire pour demain:
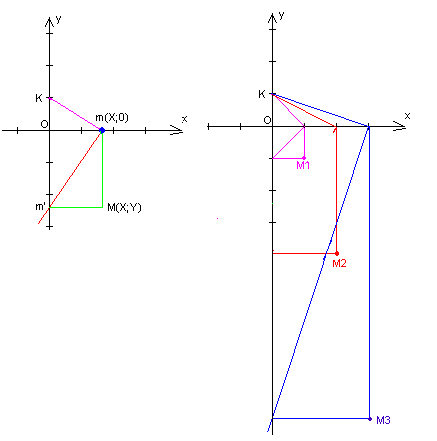
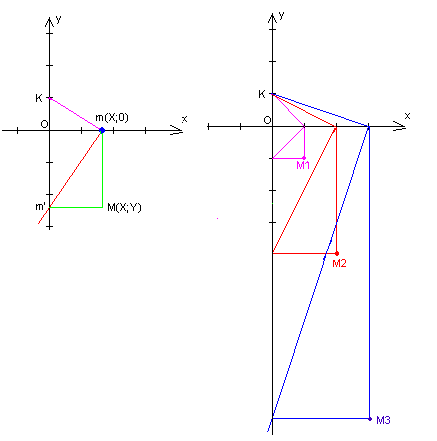
Construction de la courbe d'équation y=x²:
Le plan est rapporté à un repère orthonormal(o;i;j)d'unité 1 cm
On donne le point k de coordonnées(0;1);
m un point de l'axe des abscisses,d'absisse x.
On construit:
le point m' a l'intersection de l'axe des ordonnées et de la perpendiculaire à (Km) passant par m;
le point Mde telle maniére que OmMm' soit unrectangle.
a. Montrer,par pythagore,que les coordonnées(x;y) du point M vérifient
y=x² et donc que M est un point de la parabole d'équation y=x²
b. En utilisant la méthode précédente, construire dans le repére ci contre, ayant le centimétre comme unité, les points M1, M2, M3, de la courbe d'absisses respective 1,2 et 3.(laisser les trait de construction apparents)
a)
(Dessin de gauche)
Pythagore dans le triangle Kmm':
Km'² = Km²+mm'²
(Y+1)² = (X²+1) + mm'²
Y²+2Y+1 = X²+1 + mm'²
mm'² = Y²+2Y-X² (1)
Pythagore dans le triangle mM'm':
mm'² = mM² + Mm'²
mm'² = X² + Y² (2)
(1) et (2) ->
Y²+2Y-X² = X² + Y²
2Y = 2X²
Y = X²
-> M est un point de la parabole y = x²
-----
b)
Dessin de droite.
-----
Sauf distraction.