Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
Droite et produit scalaire.
Posté par alexman59
Bonsoir à tous.
Voila j'ai un petit exo a faire sur le produit scalaire pendant mes vacances mais sans quelques difficultés...
Il faut voir la figure pour comprendre l'exo alors j'ai mis l'image de la figure sur ce lien :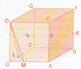 
Et je ne vois pas comment prouver que la droite (OK) est orthogonale au plan ( MDL ) Je pensais à trouver une équation de la droite et du plan , est ce que je suis bien partie ? Mais on a aucune coordonnées de point alors je suis un peu perdu...
Merci d'avance en tout cas ! 
édit Océane : image placée sur le serveur de l'
, merci d'en faire autant la prochaine fois 
Bonsoir,
Pour cet exo, as-tu le droit d'utiliser le produit vectoriel, ou seulement le produit scalaire?
En fait, tu as les coordonnées suivantes: =(-a;1;0)
=(0;1;-a)
=(1;a;1)
et
appartiennent au plan MDL.
Si l'on fait le produit vectoriel: 
on obtient un vecteur perpendiculaire à ces deux vecteurs, il reste à montrer que ce vecteur est parallèle à
C'est possible?
A ouais mais nan c'est bon. Je suis nul ! Merci ! Et Bien vu et puis on utilise la propriété une droite orthogonale à un plan si et seulement si elle est orthogonale à 2 droites sécantes de ce plan ^^ Merci beaucoup tiens peut être pourriez vous m'aider, j'ai pas mal avancé dans l'exo mais je bloque quand il demande :
3c) En déduire en fonction de a les coordonnées de H. Il doit y avoir quelque chose à faire du fait que Oh et Ok sont colinéaires mais je vois pas vraiment quoi en faite...
Salut,
Calcule OK.LM et tu demontre que le produit scalaire vaut 0
petite aide, décompose le vecteur OK avec le point B et le vecteur LM avec le point O.
Merci à vous 2 !
Pour ne pas refaire un Topic quelqu'un aurait une idée pour en déduire en fonction de a les coordonnées de H ?
Je pense démarré sur,
OH et OK Colinéaires mais je vois pas où allez -_-
Bonjour,
Citation :
Pour ne pas refaire un Topic quelqu'un aurait une idée pour en déduire en fonction de a les coordonnées de H ?
Pour ne pas refaire un Topic quelqu'un aurait une idée pour en déduire en fonction de a les coordonnées de H ?
Tu as trouvé la réponse?
Nous avons un plan défini par 3 points: M=(a;0;0) L=(0;0;a) D=(0;1;0),
[(x0;y0;z0) (x1;y1;z1) (x2;y2;z2)]
une droite définie par le point O=(0;0;0), et le vecteur directeur =(1;a;1),
[(x'0;y'0;z'0) (
;
;
]
il faut déterminer l'intersection de la droite et du plan.
l'équation du plan MDO:
u(x-x0)+v(y-y0)+w(z-z0)=0
peut s'écrire aussi:
ux+vy+wz+h=0
en remplaçant les lettres par leurs valeurs:
-ax-a2y-az+a2=0 (1)
le système d'équation de la droite:
x=x'0+
(2)
y=y'0+ (3)
z=z'0+ (4)
intersection de la droite et du plan: nous posons:
u(x'0+)+v(y'0+)+w(z'0+)+h=0
nous repartons de (1):
-a-a3-a+a2=0
=a/(a2+2)
en reportant cette valeur de dans (2)(3)(4),nous trouvons les coordonnées du pt H:
x=a/(a2+2)
y=a2/(a2+2)
z=a/(a2+2)
finalement:
=
(x2+y2+z2)
=a/
(a2+2)
Note: (développement du déterminant de la matrice des coefficients)
u=(y1-y0)(z2-z0)-(z1-z0)(y2-y0)
v=(z1-z0)(x2-x0)-(x1-x0)(z2-z0)
w=(x1-x0)(y2-y0)-(y1-y0)(x2-x0)
Désolé je n'ai pas réussi à trouver plus simple, si tu as des questions n'hésite pas, et signale-moi s'il y a des erreurs!