Bonjour à tous
J'ai un exercice à faire et je bloque à la 3 ème questions malgré mes efforts !

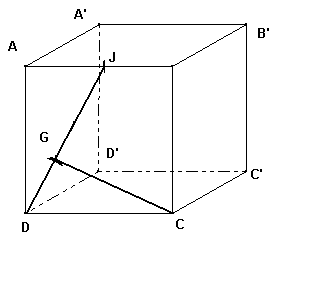
J'ai les données suivantes : ABCDA'B'C'D'' cube, J milieu de [AB] et G barycentre de (A,1) (B,1) (D,3)
J'ai démontré que :
Que : DG et DJ sont colinéaires DG= (2/5) DJ
Que : les coordonnées de G dans (0, AB, AD, AA') sont (1/5; 3/5; 0).
Que : MO+MA+3MC=5MG  (tout en vecteurs)

On m'a ensuite demandé de déterminé l'ensemble (P) des points M de l'espace suivant : (MA+MB+3MD). MC=0

Voici ma réponse : j'ai fait 5MG .MC=0 d'où MG et MB sont orthogonaux et j'ai dit que (P) est un cercle de diamètre GC cependant je ne sais pas si cette ensemble peut être une sphère ?


Voila la question ou je bloque réellement :
3) déterminer l'ensemble (H) des points M (espace) tels que :
(MA+MB+3MD).(MA+MB-2MD)=0

ICI je ne trouve pas de solution, voici mon avis :
Je peux écrire 5MG. (MA+MB-2MD)=0 ici j'ai d'abord pensé qu'on faisait intervenir un deuxième barycentre mais non car 1+1-2=0 donc il n'existe pas .
J'ai pensé alors à l'ensemble vide , mais on me demande après d'établir que DJ et CG sont orthogonaux et d'en déduire que C et C' sont deux points de (H)

Je serais très reconnaissant si vous pouviez m'aider merci !
:)