- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Ensemble de points
Bonjour bonjour !
J'ai un peu de mal avec les ensembles de points donc je fais des exos dessus mais la je ne sais pas comment faire, si vous voulez bien m'aider :
A et B sont deux points distincts de l'espace. On note I le milieu du segment [AB].
Déterminer l'ensemble des points M de l'espace tels que : (->MA + ->MB ) . -> MA = 0
Merci !
Bonjour
dans ta 1re expression (vecMA + vecMb), fais intervenir I le milieu (càd le barycentre)
ton expression va se simplifier
et le produit scalaire nul va te permettre de répondre
Bon tu vas me trouver bête si ce n'est pas déjà fait ^^ mais ok après je me retrouve avec 2vectMI.vectMA=0 mais j'en fait quoi de cette expressions ?
aucun jugement de ma part!....
2vectMI.vectMA=0 OK
soit
vectMI.vectMA=0
un produit scalaire nul, ça te dit quoi sur les vecteurs ??......
très bien!
où sont tous les points M (ici de l'espace, mais pose toi déjà la question dans le plan) tels que vecMI et vecMA soient orthogonaux ?
si dans le plan....
si dans l'espace.....
je dirais sur la médiatrice de [AB] et donc sur la droite passant par I perpendiculaire à [AB] ... :/
tu veux dire que l'ensemble des points M se trouvent sur le cercle de diamètre AI ?
Dans ce cas là c'est toujours ça ?
dans le plan
vecMI orthogonal à vecMA, c'est le cercle de diamètre IA, eh oui !
dans l'espace, c'est la sphère

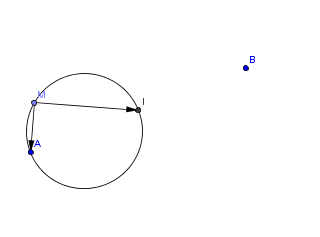
 Encore merci !
Encore merci ! 
