Salut

Ca semble logique, les entiers de gauss sont les points de coordonnées entières dans le plan complexe. Donc on peut situer a/b dans un carré de côté 1 dont la diagonale fait rac(2).

Dessine tu verras

Salut fusionfroide

Si a et b sont des entiers tout court, alors si n est un entier le plus proche du quotient a/b, alors .

a et b ne seraient-il pas supposés des entiers de Gauss quelconques ?

Kaiser

Salut Kévin

Salut Kaiser

Ah oui moi j'ai pris a/b comme un point quelconque du plan complexe...

Mais je vois pas trop comment on place a/b ??

a/b il peut être n'importe où si a et b sont des entiers de gauss comme le dit Kaiser, sinon si c'est dans Z ça n'a pas trop d'intérêt c'est sur l'axe des réels.

fusionfroide > si a et b sont des entiers de Gauss quelconques, tu peux écrire avec x et y rationnels.
Ensuite, considère m et n des entiers les plus proches de x et y, respectivement.
Considère alors q=m+in.

Kaiser

Juste pour illustrer la propriété :

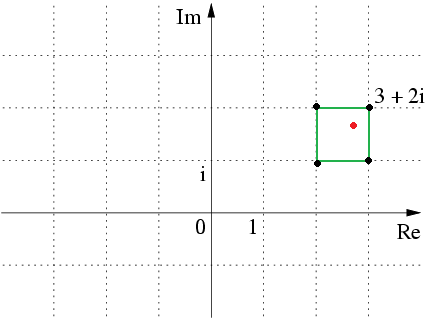
Comme l'a dit Kaiser a/b est de la forme x+iy avec x,y rationnels donc il peut être (presque) partout dans le plan complexe. On en choisit un arbitrairement (en rouge), on peut l'encadrer par un carré de côté 1 (en vert) dont les sommets (en noir) correspondent à des entiers de Gauss. On prend le sommet le plus proche de a/b (ici 3+2i) et on voit que la distance est inférieure à la demi-diagonale du carré c'est-à-dire rac(2)/2.



Voilà je vous laisse travailler, vais manger

Bon appétit !

Merci

Ok merci à vous !

Pour ma part, je t'en prie !

Pour ma part aussi (à la Kaiser )

Merci

Vieux motard que jamais...