Annuler
connectez vous
analyse complexe en post-bac
- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Equation complexe
Posté par Fractal
Bonjour,
J'ai une hésitation sur la résolution d'une équation complexe, la voici :
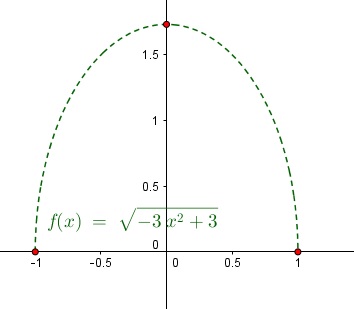
La solution serait-elle les 3 points rouges ci-dessous ?
Merci
z = x + i.y
(x - i.y)² + 2(x² + y²) - 3 = 0
x² - y² - 2ixy + 2x² + 2y² - 3 = 0
3x² + y² - 3 + 2ixy = 0
Et donc, on a le système :
3x² + y² - 3 = 0
xy = 0
a) x = 0 --> y = +/- V3
b) y = 0 --> x = +/- 1
Les solutions sont :
z1 = -V3 * i
z2 = V3 * i
z3 = -1
z4 = 1
Sauf distraction. 
il te suffit de poser z = x+iy et d'annuler les parties réelles et imaginaires de , et tu verras bien s'il existe d'autres solutions ou pas.
Bonjour,
il me semble facile de voir que z est un réel ou un imaginaire pur.
En distinguant les deux cas on trouve quatre solutions, dont les trois points que tu donnes.
Bonjour Fractal.
As-tu essayé de résoudre algébriquement ton équation ?
Si tu poses z = a+ib alors tu obtiens un système facile de deux équations à résoudre ... et à mon avis, la solution donnée est incomplète et fausse ...
Citation :
As-tu essayé de résoudre algébriquement ton équation ?
As-tu essayé de résoudre algébriquement ton équation ?
Oui
Citation :
z = a+ib alors tu obtiens un système facile de deux équations à résoudre
z = a+ib alors tu obtiens un système facile de deux équations à résoudre
C'est ce que j'ai fait.
z1 = -V3 * i <== je ne comprends pas cette solution
z2 = V3 * i
z3 = -1
z4 = 1
Celles en bleu je les avais trouvées (ce sont mes point rouges sur la figure)
salut
en notant z* le conjugué de z ...
or z + z* = 2Re z donc son carré est un réel positif donc (z* + z)^2 - 3 est un réel
donc z est réel ou z est imaginaire pur
si z est réel l'équation est 3z^2 - 3 = 0
si z est imaginaire pur l'équation est z^2 + 3 = 0
...
bonjour,
il est immédiat que si z est solution -z est solution
puisque
on peut aussi écrire
soit
on en déduit
donc
et z est réel solution de
ou
et z est imaginaire pur solution de
Bonsoir,
Solution OFF:
En termes de somme de points du plan orthonormé
la relation correspond à : (1)
-2xy= 0 ; x=0 , ,
;y=0 , ,
La relation (1) ,pour xy=0 conduit à pour la courbe support.
Alain