- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Equation d'un cercle dans C
Re-bonsoir,
Je dois trouver la représentation dans le plan complexe de l'ensemble des solutions de l'égalité :
| (z+1)/(z-1) | = 2
J'ai essayé de développer avec z = a+ib mais j'arrive à quelque chose d'assez indigeste, et je ne déduis rien du passage de z-1 de l'autre coté de l'équation..
D'après les réponses possibles du QCM, je sais que cette équation représente un cercle, mais lequel ?? Heeelp 
Bonsoir,
c'est vrai que l'on apprend plus ce genre de choses.
Un méthode possible :
En posant
Et, en principe, tu as du voir ce genre de chose.
Si tu remplaces z par a+ib ça ne donne rien d'indigeste : on apprend en Terminale à se ramener à une équation de cercle.
Autre point de vue sans les complexes:
Avec ,
et
:
Soit le barycentre de
et
le barycentre de
On obtient
décrit le cercle de diamètre
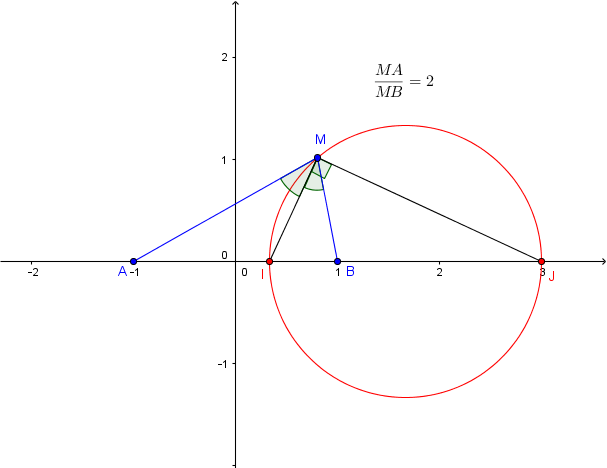



 analyse complexe en post-bac
analyse complexe en post-bac