Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Equation du 3eme degré.

Posté par
woozyx 14-10-12 à 19:00

Bonsoir ,
Je suis bloquer sur un exercice , enfin je n'ai aucune indication a par :
Trouver une solution de l'équation x3-3x+1=0  
Je ne vois absolument pas comment faire sachant que je n'ai pas vu les equations du 3eme degré si quelqu'un pourrait m'expliquer la méthode pour résoudre.
Merci d'avance

Posté par
malou Webmasterre : Equation du 3eme degré. 14-10-12 à 19:05

Bonjour
ce serait pas avec le théorème des valeurs intermédiaires ? (après une petite étude de fct) ?

Posté par
fred1992re : Equation du 3eme degré. 14-10-12 à 19:06

Bonsoir woozyx.

Te demande-t-on de, déterminer une solution explicite de cette équation ou bien de montrer qu'il en existe une ?

Ou bien, t'indique-t-on une étape à suivre ?

Posté par
woozyxre : Equation du 3eme degré. 14-10-12 à 19:23

Non , je n'ai aucune autre explications a par ce que je vous ai indiquer , apparemment il faudrait utilisé U et V , je ne vois que cette solution en réfléchissant..

Posté par
fred1992re : Equation du 3eme degré. 14-10-12 à 19:25

Bonsoir M. malou au passage...

u et v ? Mékisaysa ?

Posté par
malou Webmasterre : Equation du 3eme degré. 14-10-12 à 19:25

si c'est la suite d'un exo, où on t'a fait faire ça, effectivement....

Posté par
woozyxre : Equation du 3eme degré. 14-10-12 à 19:28

C'est des petites lettres permettant de nous aider ( apparemment ) a résoudre cette équation !
en developant x3 = (u+v)3
J'avais un autre exercice ou il fallait faire comme sa , mais toute les étapes étaient détaillées..

Posté par
woozyxre : Equation du 3eme degré. 14-10-12 à 19:32

En effet je suis tête en l'air et j'avais oublier qu'il fallait changer le -3x en + 3x
Je ne sais pas si sa change grand chose ?

Posté par
fred1992re : Equation du 3eme degré. 14-10-12 à 19:41

M. malou est certainement plus apte que moi pour répondre à ceci.

L'équation x^3 + 3x + 1 = 0 possède une seule solution réelle et 2 solutions complexes conjuguées : mais aucune d'elle n'est évidente.

Il ne me semble pas qu'on apprenne en terminale à résoudre des équations de ce type, sauf si l'énoncé te demande d'appliquer une méthode particulière.


L'énoncé complet est simplement "Trouver une solution de l'équation x^3 + 3x + 1 = 0" ?

Posté par
dhaltere : Equation du 3eme degré. 14-10-12 à 19:45

Si on te demande les valeurs exactes, il s'agit d'appliquer la méthode de Cardan.

x³-3x+1=0
pose u+v=x
développe (u+v)³
regroupe les termes tu dois aboutir à
u³+v³+3(uv-1)(u+v)+1=0

alors tu imposes uv=1, ce qui te laisse
u³+v³+1=0
uv=1

multiplie la première par u³
u^6+(uv)³+u³=0
ce qui se simplifie en
u^6+u³+1=0

tu poses U=u³, il te reste une équation du second degré
U²+U+1=0

Posté par
woozyxre : Equation du 3eme degré. 14-10-12 à 20:12

D'accord ! Je pense avoir compris ! merci beaucoup pour votre aide , j'avais aussi poster ce poste https://www.ilemaths.net/sujet-sommes-et-produit-de-deux-nombres-512490.html#msg4325060 mais personne m'a repondu concretement en tout cas merci pour votre aide , bonne soirée a vous deux

Posté par
geo3re : Equation du 3eme degré. 14-10-12 à 21:11

Bonsoir
Que ce soit pour x³-3x+1 = 0 ou x³+3x+1=0 en imposant pour la 1ère uv =1 et pour la 2ème uv = -1  on trouve U²+U+1 = 0 pour la 1ère  et U²-U+1= 0 pour la 2ème ( en posant u³ =U); mais aucune des 2 équations en U n'admet une solution réelle alors qu'une  valeur approchée de x³+3x+1=0 est x = -0.3221853546
A+

Posté par
DHilbertre : Equation du 3eme degré. 14-10-12 à 21:14

Cf. ici demonstration formule de Cardan.

A +

Posté par
dhaltere : Equation du 3eme degré. 14-10-12 à 21:26

Merci à Geo3 et à DHibert

Allez, une petite correction

résoudre (P) : x³-3x+1=0

posons x=u+v
x³=(u+v)³=u³+3u²v+3uv²+v³=u³+v³+3uv(u+v)=u³+v³+3uvx

Alors (P) est équivalente à
u³+v³+3(uv-1)x+1=0

donc si on impose en outre uv=1, (P) se simplifie
u³+v³+1=0

En multipliant par u³ on obtient

u^6+u³v³+u³=0

or u³v³=(uv)³=1³=1

u^6+1+u³=0

et en posant U=u³ on obtient

U²+U+1=0

cette équation du second degré a deux solutions complexes conjuguées
U=\frac{-1+i\sqrt3}2
ou
U=\frac{-1-i\sqrt3}2

je retiens la première, mais tu vérifieras qu'en retenant la seconde on arrive au final aux mêmes solutions de (P)

U=\frac{-1+i\sqrt3}2 peut s'écrire (on a de la chance) sous forme trigonométrique

U=e^{i\frac{2\pi}3}

ce qui nous intéresse car maintenant la condition U=u³ va pouvoir s'exprimer facilement

on utilise traditionnellement les "racines cubiques de l'unité" :
1 \\ j=\frac{-1+i\sqrt3}2=e^{i\frac{2\pi}3} \\ j²=\bar j=\frac{-1-i\sqrt3}2e^{-i\frac{2\pi}3}

tu remarqueras, mais c'est un hasard, que les deux solutions de U²+U+1=0 sont j et j²

Pourquoi ce nom, "racines cubiques de l'unité" ? parce que j³=1 (tu vérifieras)

alors soit u=e^{i\frac{2\pi}9}
on a u³=U, (ju)³=U, (j²u)³=U
ce sont les trois solutions de l'équation u³=U

et puisque on doit avoir uv=1, x=u+v, voici toutes les solutions de x³-3x+1=0

\begin{array}{|c|c|c|} \hline u & v & x \\\hline e^{i\frac{2\pi}9} & e^{-i\frac{2\pi}9} & e^{i\frac{2\pi}9}+e^{-i\frac{2\pi}9} \\\hline je^{i\frac{2\pi}9} & j²e^{-i\frac{2\pi}9} & je^{i\frac{2\pi}9}+j²e^{-i\frac{2\pi}9} \\\hline j²e^{i\frac{2\pi}9} & je^{-i\frac{2\pi}9} & j²e^{i\frac{2\pi}9}+je^{-i\frac{2\pi}9} \\\hline \end{array}
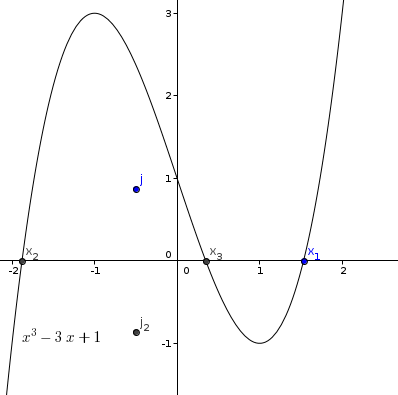
Equation du 3eme degré.
on remarque que malgré leur expression complexe, ces trois solutions sont réelles.

Posté par
dhaltere : Equation du 3eme degré. 14-10-12 à 21:30

en effet, nous avons
e^{i\frac{2\pi}9}+e^{-i\frac{2\pi}9}=2cos(\frac{2\pi}9)

je^{i\frac{2\pi}9}+j²e^{-i\frac{2\pi}9}=2cos(\frac{8\pi}9)

j²e^{i\frac{2\pi}9}+je^{-i\frac{2\pi}9}=2cos(\frac{4\pi}9)

Posté par
woozyxre : Equation du 3eme degré. 14-10-12 à 21:33

D'accord merci a tous d'avoir pris du temps pour me répondre , cela va maintenant me permettre de repondre a l'exercice d'apres plus general x3 = px + q !
Bon dimanche


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !