Inscription / Connexion Nouveau Sujet
etude de fonction
Bonsoir , j'ai la fonction suivante : f(x) = x² - 2 ln(x) - 1 .
a) Etudier ses variations .
Facile , f est décroissante sur ]0,1[ , nulle en 1 et croissante sur ]1,+infini[ .
b) Quelle est l'image de l'intervalle ]0,infini[ par f ?
Je trouve ]-infini,+infini[ , en calculant les limites .
c) vérifier que f''(x) => 2 pour x > 0 .
f''(x) = 2x²+2 / x² , donc j'ai fait
(2x²+2)/x² > 2
2x²+2 > 2x² , ici c'est évident , 2 > 0 , donc c'est ok .
d) Soit a > 1 un nombre réel . En écrivant la formule de taylor-lagrange à l'ordre 1 , sur l'intervalle [1,a] , trouver une minoration de f(a) .
Alors 1. pq à l'ordre 1 ça fait intervenir la dérivée seconde , c'est pas pareil que taylor young l'ordre ?
donc voici la formule :
f(b) - f(a) = (b-a)f'(a) + (b-a)²/2 f''(c)
en fait je ne comprends pas bien la question , si quelqu'un pouvait m'expliquer le sens svp , je vous remercie .
vu les variations de ta fonction et le fait qu'elle est continue es-tu sure de tes limites ?
(vu qu'elle a un minimum en 1)
f"(x) = 2(1+1/x²) > 2*1 tout simplement
Taylor-Lagrange c'est simplement le thé. des accroissements finis appliqué à l'ordre n
Taylor-Young c'est juste que le reste à l'ordre n est hno(1)
donc c'est simplement l'écriture du reste qui change
ensuite tu a minoré ta derivee f" et tu connais le signe de f'x) quand x>1 donc ça devrait aller

oui je suis certaine de mes limites , j'ai vérifié avec un logiciel d'ailleurs .
"Taylor-Lagrange c'est simplement le thé. des accroissements finis appliqué à l'ordre n"
oui mais alors pq l'ordre 1 fait intervenir la dérivée seconde ?
"ensuite tu a minoré ta derivee f" et tu connais le signe de f'(x) quand x>1 donc ça devrait aller"
non ça ne va pas , je ne sais pas ceux qu'ils veulent dire par minoration , une fonction ? et vu que je comprends pas du tout taylor lagrange ici et le dérivée seconde je peux pas avancer sans m'expliquer cecici...
le the des accroissements finis est f(b) - f(a) = (b-a)f'(c)
donc à l'ordre 0 tu fais intervenir ta dérivée...
à l'ordre n tu fais intervenir ta dérivée n+1
donc à l'ordre 1 tu appliques le the des af à ta dérivée donc il apparait f"
donc tu écrit : f(a) =f(1) + ...
limite: f(0)= f( )=+
)=+
ce me semble-t-il
je ne sais pas par quoi remplacer a , b et c dans la formule de lagrange pour répondre à la question...
salut tig , ah enfin un sauver , mais pq c'est [0,+infini[ vu que notre ami guitou a trouvé comme limites infini , infini , l'image c'est les limites non ?
et par hasard aurais tu une explication pour lagrange car je vais devenir folle 

L'image n'est pas forcément les limites comme tu dis, ceci n'est vrai que pour une fonction monotone.
Or ta fonction est décroissante jusqu'en x=1 puis croissante avec f(1)=0, donc à cause des limites, f est positive, et à cause de la continuité, l'image est tout l'intervalle [0;+infini[.
Lagrange à l'ordre 2 ne fait intervenir que des dérivées d'ordre 1 et 2, et l'ordre 1 ne fait PAS intervenir la dérivée seconde!
non mais ici je dois écrire la formule de lagrange à l'ordre 1 , c'est ce que j'ai fait , par quoi dois je remplacer a,b,c pour répondre à la question , je comprends mal là...
Oui, et tu l'as écrite à l'ordre 2 justement, pas à l'ordre 1!
A l'ordre 1 ça donne juste, avec
f(a) - f(1) = f'(c).
Après minorer f(a) c'est dire à quoi il est supérieur.
Il suffit donc de savoir minorer f'(c)
tig c'est curieux car dans l'exercice les professeurs disent clairement que le reste( à l'ordre 1 ) fait intervenir une valeur de la dérivée seconde .
je ne comprends guère ta formule , la formule du cours c'est :
f(b) - f(a) = (b-a)f'(a) + (b-a)²/2 f''(c) , à l'ordre 1
que fais tu du b-a du f'(a) et du reste , j'avoue que je suis complètement larguée par tes réponses , aurais tu une petite explication stp ?
et dans la correction de ces annales ils mettent clairement la dérivée seconde...
Oups pardon y a le facteur (a-1) qui est passé à la trappe!!
Je reprends, à l'ordre 1 on a f(a) - f(1) = (a-1)f'(c).
En revanche, j'ai toujours vu que la définition de T-L à l'ordre n ne fait intervenir que des dérivées d'ordre n ou inférieur.Après si tu as une autre définition dans ton cours, applique ce que tu pensais appliquer initialement, mais je suis surpris qu'ils vous aient changé les définitions habituelles!!
ben tig la correction de cette question c'est celle ci :
f(a) = f(1) + f'(1)(a-1) + f''(x)/2 (a-1)²
f(a) > (a-1)² , qu'en penses tu ?
merci tigweg , merci bcp 
par contre je peux me permettre une question : la formule de young permet d'avoir une approximation en un point , mais lagrange permet quoi ?
Avec plaisir severinette.
Exactement pour Young!
Lagrange permet d'avoir une approximation (genre encadrement, minoration, majoration) globale sur un intervalle, exactement comme ce qu'on vient d'obtenir.
De plus il permet d'obtenir assez facilement une majoration de l'erreur commise en remplaçant la fonction par son approximation sur l'intervalle considéré: c'est l'inégalité de T-L. 
merci tig t'as tjs des réponses simples et claires qui me sont utiles pour mieux appréhender les concepts  . c'est avec ce genre de réponse qui décourage pas qu'on a envie d'approfondir .
. c'est avec ce genre de réponse qui décourage pas qu'on a envie d'approfondir .
En ce qui concerne , on a
C'est donc l'ensemble des y de R tel qu'il existe un antécédent de y par f.
Graphiquement, on peut le voir comme ça : 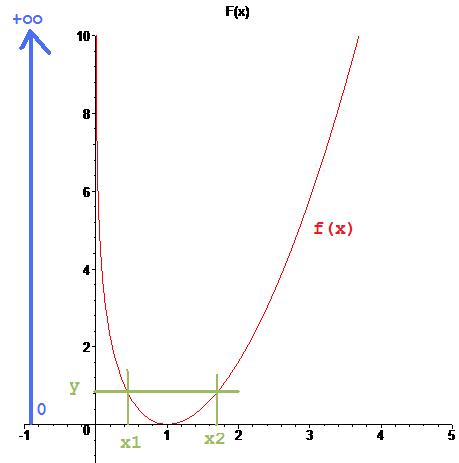
Pour tout y de , l'équation y=f(x) a au moins une solution.
Si cette équation admettait une unique solution, alors f réalise une bijection de dans
Sauf bêtise 


 analyse en Bts
analyse en Bts