Inscription / Connexion Nouveau Sujet
Comme promis, voici une solution au problème. Pour éviter les confusions liées aux maladresses de l'énoncé, je l'ai reformulé intégralement. Dans un premier temps, essaie de comprendre l'exercice et de le refaire seul. Ensuite si tu veux, on pourra discuter de ce qui te gène éventuellement.
En principe, dans la plupart des exercices, il n'y a pas de confusion possible entre confiance et risque.
Ce sont les deux faces d'une même pièce. Elles sont complémentaires : Risque = 1 - Confiance
En général le Risque est faible (1% ou 5% le plus souvent).
Donc la confiance est forte (99% ou 95% le plus souvent).
... sinon : le test n'a strictement aucun intérêt pratique.
D'ailleurs on dit souvent "prouver au seuil de x% ..." sans préciser s'il s'agit du risque ou de la confiance.
Parce que tout le monde sait que si le seuil est de 1% alors on parle de risque,
... et que si le seuil est de 99% alors on parle de confiance.
Dans la suite je note le risque et la confiance
---
On considère une population de couples de parents.
On note F la taille des femmes et H celle des hommes.
On note D = H - F la différence de taille au sein d'un couple.
On voudrait savoir si les hommes au sein des couples sont en moyenne plus grands que les femmes.
Pour cela, on tire au sort un échantillon de n=20 couples pour lesquels on calcule :
La moyenne : m = 11,18 cm
L'écart-type corrigé : s' = 10,67 cm
1. En notant la moyenne de D pour l'ensemble de la population de couples, formulez les hypothèses H0 et H1 d'un test statistique permettant d'évaluer si les hommes au sein des couples sont en moyenne plus grands que les femmes, en précisant s'il s'agit d'un test unilatéral ou bilatéral.
Test unilatéral, car on veut prouver que les hommes sont (en moyenne) plus grands au sein du couple :
2. Calculer sur l'échantillon la statistique :
3. En supposant que la distribution de D est gaussienne, préciser la loi suivie par T sous l'hypothèse H0.
Sous H0, T doit suivre une loi de Student à n-1 = 19 DDL
4. Déterminer la valeur critique du test au seuil de risque
.
Dans la table, au croisement de la ligne
... avec la colonne
... on trouve
5. Conclure le test en précisant le niveau de confiance.
on rejette H0 au seuil de confiance 99%
6. Cette conclusion confirme-t-elle l'affirmation des sociologues selon laquelle :
"les femmes ont tendance à avoir des enfants avec des hommes plus grands qu'elles" ?
Le test prouve (au seuil de 99%) que les hommes sont en moyenne plus grands au sein d'un couple.
Mais le test ne permet pas d'expliquer la raison de ce constat.
En particulier, il ne permet donc pas de confirmer l'affirmation des sociologues
... si celle-ci suppose que ce sont les femmes qui déterminent cette différence de taille.
Du reste, les hommes étant plus grands que les femmes en général, les femmes n'ont guère
d'autre choix que d'avoir des enfants avec des hommes "en moyenne plus grands qu'elles".
Et donc le test ne fait que confirmer quelque chose qu'on sait déjà...
VARIANTE BILATERALE...
La question posée au départ est de savoir si il y a une différence de taille en faveur d'un des deux sexes.
1. Hypothèses :
Ici, il s'agit d'un test bilatéral, car on ne fait aucune supposition a priori sur le sexe qui aurait la plus grande taille en moyenne. Dans le cas des humains, cette hypothèse est étrange car on "sait déjà" que les hommes sont plus grands. Mais on peut imaginer qu'il s'agit d'une population nouvelle découverte sur une île inconnue ou sur une planète habitée, ou bien qu'on étudie des animaux...
Donc aucun a priori : la différence D peut aussi bien être positive que négative en moyenne...
test bilatéral
2. Statistique de test :
La statistique de test reste inchangée : Tech ~ 4.69
3. Loi de T :
Inchangée : Sous H0, T suit une loi de Student à n-1=19 DDL.
4. Valeur critique Tc au seuil de 1% :
Là il y a du changement...
Si le risque est de 1%, dans un test bilatéral il sera réparti :
pour moitié (donc 0.5%) "à gauche" (pour les valeurs fortement négatives de D)
pour moitié (donc 0.5%) "à droite" (pour les valeurs fortement positives de D)
Donc il y aura deux seuils critiques opposés : Tc1 = -Tc2.
Tc2 se lira dans la table au croisement de la ligne DDL=19 avec la colonne 0.995 = 1 - 0.01/2
On trouve : Tc2 = 2.86
Tc1 ne se lit pas dans la table en pratique, puisque c'est juste l'opposé de Tc2, donc Tc1 = -2.86
NB : la table fournie avec l'exercice ne présente pas cette colonne.
5. Conclusion du test :
Inchangée : on rejette H0 au seuil de confiance 99%
6. Confirmation de l'affirmation des sociologues :
Inchangée : le phénomène est statistiquement avéré (il y a une différence moyenne de taille significative au seuil de 99%) mais aucune raison n'est mise en évidence.
5. Conclusion du test (rectificatif) :
Inchangée : Tech est en dehors de l'intervalle [ Tc1 ; Tc2 ] donc on rejette H0 au seuil de confiance 99%
Merci à toi.
Il y a juste quelque chose que je ne comprends pas : comment je sais si dans le tableau la colonne représente le risque ou le niveau de confiance ?
Par exemple dans cet exercice s'il représente le niveau de confiance (ce qui est donc la réalité) je dois lire dans la colonne 0,99.
Mais si le tableau représentait le risque pour les colonnes j'aurais dû lire la colonne 0,01 donc j'aurais eu -2,54, ce qui change tout !
On peut te donner différentes tables.
Mais dans chaque cas, tu auras une définition qui te permettra d'en connaître la signification.
Souvent cela ressemblera à : P(T<valeur) = probabilité
Cette probabilité peut être notée alpha, ou alpha' ou 1-alpha... cela dépend.
Pour la table : alpha (ou alpha' ou 1-alpha ou autre...) : c'est juste une probabilité.
A ce stade ce n'est donc ni une confiance ni un risque.
Ce n'est que lors de l'application d'un test que cette probabilité prendra un sens en rapport avec le test effectué.
Par exemple :
Si la table mentionne : P(T<x) = alpha' = 1 - alpha...
... alors cet alpha coïncidera avec le risque (et alpha' la confiance) pour un test unilatéral.
Pourquoi ?
Parce que P(T<x) = 1 - alpha ==> P(x<T) = alpha
Or si H0 est vraie, et que ton échantillon te fournit un Tech > Tc tu seras pile dans le cas où tu vas rejeter par erreur.
Si ça te parait compliqué, et que tu es dans l'urgence regarde simplement les valeurs et essaie de "sentir" ce qui se passe. Et normalement tu devrais faire le bon choix.
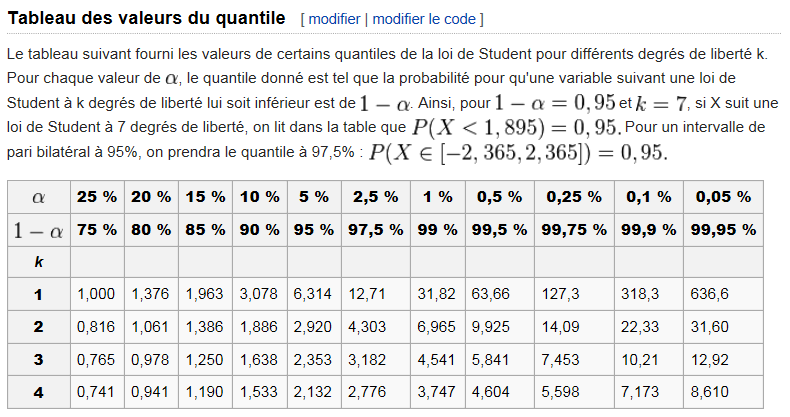
Voici ci-dessous à quoi ressemble la table proposée sur Wikipédia...
Va la voir.
Et ensuite fais ma version de l'exercice.
Je suis certain que tu devrais y arriver.
![]()
En tout cas ça me fait bien détester les stats tout ça...
Et moi je jure à chaque fois que je ne ferai plus de statistique par correspondance...
... parce que c'est impossible.
C'est une belle discipline. Elle mérite le respect. Et pour la maîtriser il y a des étapes. Quand on veut les brûler... on se brûle aussi les ailes.
Je sais que tu es dans l'urgence. Comme les autres je respecte ta démarche.
Mais tes difficultés viennent essentiellement de ce que tu ne joues pas le jeu.
Ok je vois, merci.
Je pense que je vais faire en "sentant" comme tu dis.
Par exemple dans cet exercice si j'avais lu dans la colonne 0,01 j'aurais obtenu -2,54 en valeur critique.
Et donc sur le graphique j'aurais vu que -2,54 c'était trop "vers la gauche" par rapport à 4,69, c'était d'ailleurs ce qui me perturbait lors de la rédaction de mon sujet.
Donc ici j'aurais pu voir que c'est bizarre et lire dans la colonne 0,99 à la place.
Je vais réessayer de faire l'exo tout seul tout à l'heure.
Je me permet de citer ce message d'alb12 posté hier et qui est peut-être passé inaperçu...
Il résume très bien les situations que tu pourrais rencontrer en examen (et alb12 a probablement plus d'expérience que n'importe lequel d'entre nous sur ces sujets...).
Imaginons que tu tombes sur un test de comparaison de 2 moyennes
H0 et H1... tu sais faire
Valeur observée... tu sais faire (calcul de la statistique de test appropriée à la situation)
Ensuite valeur théorique : ici X sera variable normale ou de Student
Si bilateral : chercher Tth tel que P(X<Tth)=1-risque/2 = 0.975 (si risque 5%) ou = 0.995 (si risque 1%)
Si unilateral : chercher Tth tel que P(X<Tth)=1-risque = 0.95 (si risque 5%) ou = 0.99 (si risque 1%)
Si valeur observee dépasse valeur théorique : alors on rejette H0 (en conclusion : on affirme H1, au seuil fixé).
Si valeur observée inferieure à valeur théorique : alors on ne rejette pas H0 (en conclusion on accepte H0, au seuil fixé)
Avec ça tu as l'essentiel.
Par exemple dans cet exercice si j'avais lu dans la colonne 0,01 j'aurais obtenu -2,54 en valeur critique.
Et donc sur le graphique j'aurais vu que -2,54 c'était trop "vers la gauche" par rapport à 4,69
Bingo
 !
!
C'est EXACTEMENT à ça que je pensais quand je te disais de suivre ton instinct (faute de mieux).
Et relis le message d'alb12 que j'ai reposté à l'instant... Il est simple, clair, précis.
Ca pourrait t'aider.
Merci à vous tous, je pense que ça s'est plutôt bien passé.
Je vous tiendrai au courant de ma note si je n'oublie pas (vers début juillet je pense).
Bonjour à tous,
Comme promis je viens donner des nouvelles.
J'ai donc eu 15/20 (et 16 à l'UE grâce aux TP).
Merci pour votre aide.



 statistiques en post-bac
statistiques en post-bac