Salut
essaie de montrer que 2x<1+x² et que -2x<1+x² alors tu pourras montrer que f(x) est compris entre -1 et 1
Ensuite tu sais que cette fonction est continue pour qu'elle soitsurjective il faut qu'elle atteigne les valeurs 1 et -1 et ensuiute par le th des valeurs intermédiaire tu pourras conclure
reste a montrer que f atteint les valeurs 1 et -1 a toi de chercher
si tu ne trouves toujours pas reposte dansle même topic

salut Doe

Outre les explications de titimarion, tu peux aussi étudier la fonction f sur R ...





      

Là , tu fais un tableau de variation :



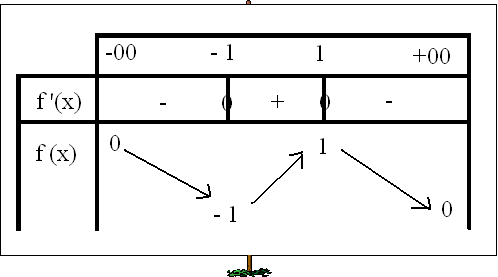
tu constates donc que f(x) est bien compris entre -1 et 1

++ sur l'

f' est bien définie en -1 et 1 non?

>> otto 16:19

oui pourquoi, j'ai dis une bétise ?

Non tu ne t'es pas trompé, mais ce sont les barres sur les 0 du tableau qui peuvent mettre le doute.

A d'accord escuse moi , j'ai l'habitude de faire comme ça, mais c'est vrai que si je me souviens bien, normalement on fais comme ça :



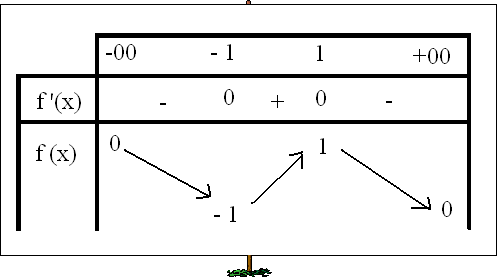
Tu préfères

++ sur l'

titimarion
lyonnais
otto

Je vous remercie d'avoir été aussi rapides et pour votre aide.
Le site est super ! Je suis très content de l’avoir trouver.

P.S.

Je vais essayer de résoudre la suite de l’exo

Pourquoi tu repostes mes deux superbes tableaux océane ?

pour les mettre sur le serveur

cool ...

ces choses là me dépassent, mais je te donne mon accord

Même si je crois que tu n'en as pas besoin !

++ sur l'

lyonnais

Comment on fait pour trouver les zeros de 2(1-x)(1+x)/(1+x²)² ?
Vu que 1+x² nous donne +/- i

Les "zéros" de 2(1-x)(1+x)/(1+x²)² sont les valeurs de x qui permettent d'annuler cette fraction. Il s'agit donc d'annuler le numérateur 2(1-x)(1+x) pas le dénominateur (1+x²)².

Et les x qui annulent 2(1-x)(1+x) ne se voient-ils pas immédiatement ?

Nicolas

Au contraire, le dénominateur (1+x²)² doit rester toujours non nul, sinon, la fraction n'est plus définie !

Nicolas

exact Nicolas_75

merci d'avoir répondu pendant mon abscence ...

++ sur l'

Bien sur comme le dit lyonnais on peut passer par le calcul de la dérivé pour obtenir le résultat cependant cela peut entrainer des erreurs de calcul.
cette méthode est bien sur la plus utilisé pour értudier une fonction, cependant dans le cas de cet exercice il est quand même beaucoup plus aisé de vérifier à la main puisqu'on tombe sur les identités remarquable et cela évite tout calcul.

Bonjour,

a)Montrer que pour tout x de R , f(x) est compris entre –1 et 1

Une autre façon de faire est de dire :

A) f(x)>-1

2x = 2x + (1+x²) - (1+x²) = (2x + 1 + x²) - (1+x²) = (1+x)² - (1+x²)
donc
f(x) = ( (1+x)²-(1+x²) )/(1+x²) = (1+x)²/(1+x²) - 1 = -1 + terme positif

donc f(x) > -1 quelquesoit x

B) f(x)<1

2x = -(-2x) = -( -2x + (1+x²) - (1+x²) ) = -(-2x+1+x²) + (1+x²) = -(1-x)² + (1+x²)
donc
f(x) = (-(1-x)²)+(1+x²) )/(1+x²) = -(1-x)²/(1+x²) + 1 = 1 - terme positif

donc f(x) < 1 quelquesoit x

Philoux

>Re

Une autre façon de faire est encore de dire :

f(x)= 2x/(1+x²) (Ca fait penser à de la trigo, non ?)

si on pose x=tan(),

qd varie de -pi/2 à pi/2, x varie sur R : pas de soucis.

or, on sait que sin(2) = 2tan()/(1+tan²())

donc f(x)=sin(2)

Comme :
-pi/2 < < pi/2
-pi < 2 < pi
-1 <= sin(2) <=1 ( la valeur 0 atteinte pour = 0 et non pour = pi )

Philoux

philoux tu t'amuses quand même à faire trèscompliqué pour montrer quelquechose de très simple.
Je suis sur que si tu cherches encore un peu tu vas trouvé une méthode encore plus tordue pour arriver au résultat

Salut titimarion

Je ne crois pas...

C'est, en fait, ta remarque de 15:30 qui m'a incité à me chercher sans passer par la dérivée.

D'où, initialement, le post de 17:19.

Par suite, je me suis souvenu d'un exo avec calcul intégral qui avait une fonction de ce type.

Par ailleurs, montrer qu'une fonction est comprise entre -1 et 1 doit faire penser à du changement de variable trigo, non ?

Ca peut aider certains élèves à avoir ce réflexe avec des exos de ce type.

Ces deux derniers posts sont là pour montrer qu'on peut faire autrement que par l'artillerie "lourde" : dérivée...

Mais ta remarque est aussi justifiée...

Philoux

Je suis d'accord en effet mais le changeent de variable par tan est quand même assez lourd, en plus tu n'a pas besoin des quelques lignes d'étude sur theta, une fois que tu obtiens ta formule sous forme de sinus tun'as plus qu'a conclure.
Mais cela force à connaitre ses formules de trigo ce qui est parfois utile mais un peu compliqué pour résoudre cet exo quand même.
Mais je ne critique en aucun cas, c juste qu'en général j'essaie de faire au plus simple.

>titimarion

en plus tu n'a pas besoin des quelques lignes d'étude sur theta

Il faut quand même s'assurer que le changement de variable respecte le domaine de variation initial de x, non ?

Quant au choix, tan(theta) plutôt qu'autre chose (tan(théta/2)..), c'est la formule 2x/(1+x²) qui le veut.

Dernièrement, un des mathîliens (toi ou otto ou ?) m'a parlé des "règles" de Bioche vues en sup/spé (?) pour du calcul intégral; Ces formules de transformation sont/seraient donc à connaître ?

Philoux

Quand je disais qu'il ne fallait pas s'occuper de theta c'est pour tes dernières lignes

Comme :
-pi/2 < < pi/2
-pi < 2 < pi
-1 <= sin(2) <=1 ( la valeur 0 atteinte pour = 0 et non pour = pi )

Bien sur qu'il faut vérifier que le domaine d'étude est inchangé.

en ce qui concerne les règles de Bioche ca devait etre avec Otto, c'est formule sont en effet à connaitre mais en général on les utilise pour faire du calcul d'intégral et non pour étudier une fonction.

Ok merci

Philoux

Bonjour,

Oui c'est otto qui a parler des règles de bioche. C'est pour choisir le bon changement de variables à faire pour calculer une intégrale. C'est plus a voir comme une astuce !

Amicalement,

Bonjour titimarion et jmix90

Rendons à César ce qui appartient à Jules !

Il s'agissait de aicko qui répondait à mes questions de béotien : besoin d aide pour intégration d une fonction assez complexe

Otto a aussi complété dans le même post.

Merci encore,

Philoux

Nicolas_75
En effet ce que je voulais dire ce que je trouve pas les même singes dans le tableau de variation

Dans le tableau de lyonnais il y a

–00       –1            1         +00
      -            +          -    

Moi je trouve

–00       –1            1         +00
      +           -            +    


Car
                        –00       –1            1         +00

               1+x            -           +            +
               1-x            -           -            +
        2(1+x)(1-x)           +           -            +          

>Doe 17:03

Une ptite erreur dans ton tableau :

Car
                        -00       -1            1         +00

               1+x            -           +            +
               1-x            +           +            -   (x est précédé du signe moins)

Philoux

Bonjour tout le monde,une petite intrusion:
on peut voir aussi que:
donc avec égalité ssi

C vrai elhor mais encore  faut il savoir que ce rapport entre la moyenne géométrique et la moyene arithmétique est inférieur à 1, ce qui est il me semble plus compliqué que l'exercice en lui même.

Bonjour,

rapport entre la moyenne géométrique et la moyene arithmétique est inférieur à 1

Merci d'avoir trouvé plus compliqué

Trèves de jokes, cela se démontre-t-il autrement que par simplification du rapport ?

Philoux

Une façon de le montrer est de montrer que
ce qui est assez évident puisque le terme de droite est égale à celui de gauche plus une certaine somme d'éléments positifs si l'on a considéré que tous les termes étaient positifs

RAS.Tout a déja été écris

Salut tout le monde,Titimarion je n'ai pas compris ce passage:
"ce qui est assez évident puisque le terme de droite est égale à celui de gauche plus une certaine somme d'éléments positifs si l'on a considéré que tous les termes étaient positifs"
veux-tu l'éclaircir s'il te plait.Merci

J'ai dis une grosse betise car je n'avais pas vu mon que le 1/n était aussi à la puissance n ce qui a causé mon erreur, je me disais aussi après coup que ce n'était pas aussi simple.
J'avoue que je ne me souviens plus de la démo dans le cas général dans le cas n=2 c'est évident mais le cas général faut que je réfléchisse un peu,  a moins que tu es la solution elhor?
Encore désolé pour l'énormité que j'ai écrite

Salut Titimarion,il est vrai que le terme figure dans l'expression et plus précisément il figure exactement fois,on le retrouve donc avec le coefficient multiplicatif dés que .
pour montrer l'inégalité dans le cas général on utilise le fait que la fonction: est convexe car les étant strictement positifs on peut trouver des réels tels que il vient alors que:

Voilà et il se peut qu'il y ait une preuve plus simple que ça

> Philoux

Pour le rapport de la moyenne geometrique et de la moyenne arithmetique de deux reels positifs, ca ne me parait pas si complique que ca. je dirais meme que c'est un classique:



en divisant par 4



donc

car le deuxieme terme est positif

en passant a la racine le tour est joue...

... ce qui revient en fait a faire la demo de titimarion du tout debut...

Un peu bizarre mon latex...
Les carres osnt pas super visibles. Enfin tout le monde aura compris...

Merci biondo 00:27

la démo, pour 2 valeurs a et b, est en effet astucieuse ...

pour n valeurs, j'ai du mal à suivre...

Philoux

Merci elhor, j'avais pensé a une preuve utilisant la concavité du log, ce qui revient au même, cependant habituellement la convexité on la voit de cette manière la
la il faut la généraliser par récurrence.
Pour le cas n=2 pas vraiment besoin d'astuce en effet si tu consideres

>salut titimarion

Qu'est-ce que la "convexité" ?
En rapport avec concave/convexe d'une courbe ?

et que signifie f(tx+(1-t)y) ?

Merci pour la vulgarisation

Philoux

Salut
la convexité d'une fonction a en effet un rapport avec la convexité d'une courbe.
il y a pluseurs definitions équivalentes nottament on retrouve que son graphe représente une courbe convexe.
Une des définitions et que pour tout et pour tout (x,y)
Alors

Il faut lire

Oui Philoux, la convexite d'une fonction, c'est la convexite de sa courbe representative (vulgairement...).

Si tu fais varier t de 0 a 1, l'expression tx + (1-t)y represente en fait un parametrage du segment [x,y], et donc l'inegalite veut dire que la courbe representative de la fonction, sur le segment [x,y], se trouve "sous" la droite reliant les points (x;f(x)) et (y;f(y))...

Je suis pas fort pour les schemas, je te laisse le faire sur un papier chez toi.

Merci beaucoup à tout les deux

Je comprends mieux l'introduction du t et l'utilisation du y (que je prenais initialement pour y=f(x) )

Il eut été moins ambigü d'écrire f(tx₁+(1-t)x₂)>tf(x₁)+(1-t)f(x₂)

Merci encore

Philoux

désolé si j'ai mis et pas c'est juste que la notation y=f(x) n'est utilisé qu'au Lycée, et donc ca fait un moment que je ne l'utilise plus, pour moi il n'y avait donc rien d'ambigüe dans mes propos, je comprends que cela t'es gêné mais en même temps il faut savoir que ce ne sont que des notations j'aurais pu prendre ou tout autre couple cela fonctionne aussi.

tout à fait titimarion 11:19

C'est vrai :quand on comprend ce que l'on manipule, on peut donner n'importe quelle lettre.

Mais je ne voyais pas, à première lecture, la signification géométrique/analytique de tx+(1-t)y
=> l'explication de biondo (la signification du t) a complété ton post.

Merci encore

Philoux