Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup TopologieTopics traitant de topologie [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Exercice monotonie à partir d'un certain rang

Posté par
DreamBoy 07-03-20 à 18:36

Bonjour,

Je souhaite de l'aide à propos de la résolution de l'exercice suivant :

Soient a un réel positif et (xn)n la suite définie telle que x0 0 et pour tout n ,
xn+1 = xn2 + a/(n + 1).

Je dois étudier la suite.

J'ai traité le cas a = 0 : j'ai pour tout n , xn = x2^n. La suite (xn) est extraite de (x0n).
Si x0 = 1 alors lim(xn)=1.
Si x0 1 alors lim(xn)= + .
Si x0 1 alors lim(xn)=0.

Ensuite pour le cas a > 0, notre prof nous a dit de montrer tout d'abord que la suite est monotone à partir d'un certain rang (ce qui pourra aider pour le calcul de limite avec le theoreme de la limite monotone). Cependant je coince.
J'ai calculé xn+1 - xn or ce calcul ne mène pas à grand chose.

Merci beaucoup de votre aide à l'avance.

Posté par
cerveaulogikre : Exercice monotonie à partir d'un certain rang 07-03-20 à 18:42

Bonsoir,
Que se passe-t-il avec \dfrac{x_{n+1}}{x_n} ?

Posté par
cerveaulogikre : Exercice monotonie à partir d'un certain rang 07-03-20 à 18:58

Je ne suis pas sûr que ma remarque ci dessus soit bonne, et je m'en excuse

Posté par
carpediemre : Exercice monotonie à partir d'un certain rang 08-03-20 à 01:39

salut

x_{n + 1} = x_n^2 + \dfrac a {n + 1}

tout d'abord il serait bien de remarquer/démontrer que la suite (x_n) est positive !!!

x_{n + 1} - x_n = x_n^2 - x_n + \dfrac a {n + 1} = \left(x_n - \dfrac 1 2 \right)^2 - \left( \dfrac 1 4 - \dfrac a {n + 1} \right)  ouais bof ... à voir ...

x_{n + 2} - x_{n + 1} = x_{n + 1}^2 - x_n^2 + \dfrac a {n + 2} - \dfrac a {n + 1} = (x_{n + 1} - x_n)(x_{n + 1} + x_n) - \dfrac a {(n + 1)(n + 2)}

ouais bof ... la seule chose qu'on puisse dire c'est que si il existe un rang pour lequel x_{n + 1} - x_n \le 0 alors la suite est décroissante à partir de ce rang ...

Posté par
carpediemre : Exercice monotonie à partir d'un certain rang 08-03-20 à 13:42

as-tu essayé de regarder avec un tableur pour différentes valeurs de a et x_0 pour voir ce qui se passe ?

Posté par
luzakre : Exercice monotonie à partir d'un certain rang 08-03-20 à 17:31

Bonsoir !
Il est maladroit d'écrire

Citation :
La suite (xn) est extraite de (x0n).

x_n est un réel, pas une suite.

........................
Il est immédiat que si x_p\geq1 la suite est croissante pour n\geq p.
Reste à voir si on peut avoir : \forall n\in\N,\;0\leq x_n\leq 1 ?
Je cherche encore dans ce sens en remarquant que les valeurs d'adhérence ne peuvent être que 0 ou 1.

Posté par
KNO3re : Exercice monotonie à partir d'un certain rang 08-03-20 à 18:40

alors c est dur la prepa?

Posté par
luzakre : Exercice monotonie à partir d'un certain rang 10-03-20 à 08:41

Il me reste un point noir !
Je suppose a>0.

En suivant carpediem :
1. Il existe un entier p tel que u_{p+1}\leq u_p.
Alors, \forall n\in\N,\;n\geq p\implies u_{n+1}\leq u_n : la suite est décroissante à partir du rang p.
A noter que forcément u_p<1.
En effet, si u_p\geq1 il vient u_{p+1}>u_p et la suite est croissante.
Par conséquent la suite est décroissante à partir du rang p,  minorée par 0 donc converge et la limite (nécessairement dans [0,u_p]) est nulle.

2. Pour tout entier n on a u_{n+1}\geq u_n
La suite est croissante.
Si elle converge la limite est nécessairement dans [u_1,\to[ et vaut 1 (car u_1>0).

Ma question
Je ne sais pas montrer, dans le cas 2. qu'il existe une valeur de la suite supérieure à 1, auquel cas elle serait divergente , de limite +\infty
ou que les valeurs sont toutes inférieures (strictement) à 1, auquel cas la suite est convergente de limite 1.

Il est évident qu'il est toujours possible de choisir u_0 tel que u_1>1 et avoir une suite divergente.
Mais pour a,u_0 donnés je ne vois pas la certitude d'un confinement à [0,1[ ni la certitude d'une sortie de cet intervalle.

Posté par
Sylvieg Moderateurre : Exercice monotonie à partir d'un certain rang 10-03-20 à 13:58

Bonjour,
Une piste peut-être ?
Si n+1 > 4a \; alors \; il existe r supérieur à 1 solution de \; x = x2 + a/(n+1) .

On a alors \; xn+1-r = (xn-r)(xn+r) .

Ça pourrait donner \; xn+1 > xn \; car \; xn+r > 1 .
A vérifier.

Posté par
Sylvieg Moderateurre : Exercice monotonie à partir d'un certain rang 10-03-20 à 14:01

Aïe : r supérieur à 1...

Posté par
Sylvieg Moderateurre : Exercice monotonie à partir d'un certain rang 10-03-20 à 14:27

Oubliez mes messages.
(un) monotone à partir d'un certain rang a déjà été démontré dans les précédents messages...

Posté par
DreamBoyre : Exercice monotonie à partir d'un certain rang 11-03-20 à 00:52

Bonsoir,

j'ai avancé de mon coté et tout d'abord j'ai quelques questions avant de vous montrer mes démarches :

carpediem @ 08-03-2020 à 01:39

ouais bof ... la seule chose qu'on puisse dire c'est que si il existe un rang pour lequel x_{n + 1} - x_n \le 0 alors la suite est décroissante à partir de ce rang ...

Je ne comprends pas en quoi les calculs que vous avez avancés montre cela.


Voici ce que j'ai fait depuis :

(Rappel a>0 et x_{0}\geq 0)

Tout d'abord, (x_{n}) est une suite à nombres positifs.

1. Si x_{0} \geq 1 alors x_{1} = x_{0}² + a > x_{0} \geq 1 d'où x_{1} > 1, ainsi en supposant x_{1} > 1 j'ai x_{2} > x_{1} > 1. Et par récurrence, on a pour tout entier naturel non nul, x_{n+2} > x_{n+1} > 1. (x_{n}) est décroissante à partir du premier rang.

2. Supposons x_{0}\in ]0 , 1[.
Dans le cas où a\geq 1, je conjecture que la suite est croissante à partir du rang 1 et diverge en + infini.
Dans le cas où 0 < a < 1 : J'ai trouvé que si x_{0} \geq \sqrt{1-a} alors x_{1} \geq1.
Si x_{0} \geq \sqrt{\sqrt{1-a}-a/2} alors x_{2} \geq1.
Et vite fait, si x_{0} \geq\sqrt{\sqrt{ \sqrt{\sqrt{\sqrt{\sqrt{1-a}-a/2}-a/3}-a/4}-...}-\frac{a}{p}} alors x_{p} \geq1.
Bref c'est pas fou mais en tout cas je reviens à un certain rang p où x_{p} \geq1 et ainsi par analogie à (1.), pour tout n supérieur à p+1, x_{n+1} > x_{n} > 1, (x_n) est croissante à un certain rang (c'est ce que vous aviez dit carpediem et luzak mais je n'avais pas compris vos démonstrations pour justifier cela).

Je n'ai vraiment que peu écrit et pas trop détaillé les calculs. Je vais montrer la conjecture dans le cas où a\geq 1, la suite est croissante à partir du rang 1 et diverge en + infini.

Je vous tiendrai au courant.

En tout cas, MERCI BEAUCOUP à vous tous de m'aider car cet exercice n'est vraiment pas facile à faire.

Posté par
Sylvieg Moderateurre : Exercice monotonie à partir d'un certain rang 11-03-20 à 07:28

Bonjour,
Je réponds pour

Citation :
Je ne comprends pas en quoi les calculs que vous avez avancés montre cela.

A partir de cette égalité :
x_{n + 2} - x_{n + 1} = (x_{n + 1} - x_n)(x_{n + 1} + x_n) - \dfrac a {(n + 1)(n + 2)}
a est positif, les x_n sont positifs.
Donc si x_{n + 1} - x_n est négatif alors x_{n + 2} - x_{n + 1} aussi.

Posté par
DreamBoyre : Exercice monotonie à partir d'un certain rang 11-03-20 à 08:09

Ah ok merci, je n'ai pas percuté tout de suite. Ça pourra m'aider. Merci Sylvieg.

Posté par
DreamBoyre : Exercice monotonie à partir d'un certain rang 11-03-20 à 22:20

Bonsoir, j'ai une effectué une démonstration de tout l'exo cependant je n'ai pas explicitement donné les conditions sur a et x_0 dans le cas où x_0 < 1.

Supposons a > 0. (x_n) est une suite à éléments tous positifs.


Si (x_n) est monotone (à partir d'un certain rang) alors admet une limite finie ou égale à + ou -. Si (x_n) est convergente vers , d'après la relation, à la limite ² = d'où = 0 ou = 1.


Supposons x_0 1. Alors x_1 = x_0² + a > x_0 1. En particulier x_1 > 1. x_{2} = x_{1}² + \frac{a}{2} > x_{1} > 1 d'où x_{2} > x_{1} > 1. Je montre par récurrence que pour tout entier naturel non nul n, x_{n+1} > x_{n} > 1.
(x_n) est (strictement) croissante donc d'après le théorème de la limite monotone, elle a une limite en 0, 1 ou +. Or n 1, (x_n) > 1 donc (x_n)+.

Supposons x_0 [0, 1[. Ou (x_n) est croissante ou il existe p tel que x_{p+1} \leq x_{p}.

Supposons qu'il existe p tel que x_{p+1} \leq x_{p}.
x_{p}² + \frac{a}{n+1} \leq x_{p} < x_{p} + \frac{a}{n+1}
x_{p}² < x_{p}.
Ainsi 0< x_{p}<1.

Ainsi x_{p+1} < x_{p}<1.
Je montre par récurrence que pour tout n p, x_{n+1} < x_{n}<1. (xn)np est décroissante à valeurs < 1 et minorée par 0. D'après le théorème de la limite monotone elle converge et admet pour limite 0 (seule limite possible).

Après dans le cas (x_n) croissante c'est l'impasse, je conjecture avec Excel que lorsque (x_n) est croissante, il existe des valeurs de (x_n) > 1 qui font diverger la suite vers +. J'ai essayé de raisonner par contraposition puis par l'absurde en supposant (x_n) croissante et en prenant pour vrai l'hypothèse x_n 1. Cependant je n'y arrive pas mais j'ai l'intime sentiment que cette piste peut être bonne.

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 12-03-20 à 08:45

Bonjour à tous.

t et a étant deux réels positifs, je note  (x_n(a,t))_{n\in\mathbb N}  la suite définie par:

x_0(a,t)=t   et     \forall n \in \mathbb N \ , \ x_{n+1}(a,t)=x_n(a,t)^2 +\dfrac{a}{n+1}

J'ai réussi à démontrer le résultat suivant:

Citation :

Pour tout réel t de [0,1[, il existe un unique réel \alpha(t)>0 tel que:

0\leq a < \alpha(t) \Longrightarrow \lim_ {n\rightarrow +\infty} x_n(a,t)=0
a = \alpha(t) \Longrightarrow \lim_ {n\rightarrow +\infty} x_n(a,t)=1
a > \alpha(t) \Longrightarrow \lim_ {n\rightarrow +\infty} x_n(a,t)=+\infty


La démonstration n'est pas très difficile mais elle est assez technique (il faut prendre le temps de comprendre les idées et les notations).

Souhaitez-vous que je rédige la démonstration ?
Ou préférez-vous que je donne des indications ?
Peut-être faut-il transférer le sujet dans le forum "détente" ...

Posté par
Sylvieg Moderateurre : Exercice monotonie à partir d'un certain rang 12-03-20 à 09:18

Bonjour,
Bravo d'avoir trouvé quelque chose
Je propose qu'on attende que DreamBoy s'exprime.

Posté par
luzakre : Exercice monotonie à partir d'un certain rang 12-03-20 à 11:16

Bonjour perroquet !
Ta démonstration m'intéresse !
Et j'aimerais surtout savoir si ta fonction \alpha a une réciproque ce qui permettrait, pour un a donné, connaître selon le choix de x_0 le comportement de la suite.

Posté par
XZ19re : Exercice monotonie à partir d'un certain rang 12-03-20 à 17:42

Bonjour
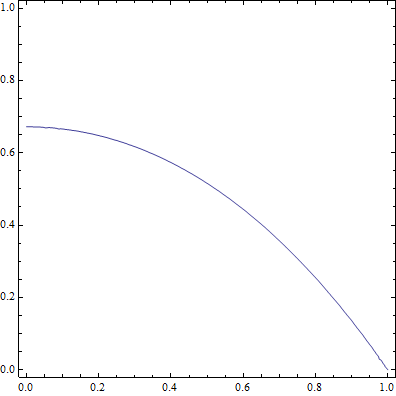
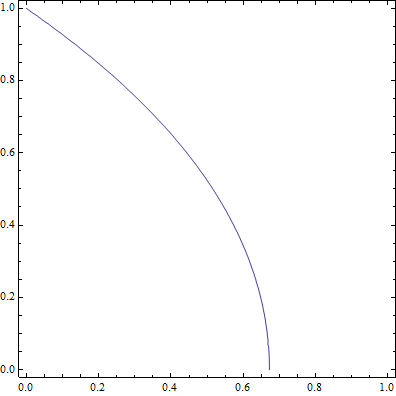
Sans  trahir  la démonstration de @Perroquet, voici le graphe  de la fonction \alpha  et de sa réciproque.  

Une question se pose concernant  la régularité de cette  fonction?  Est-elle continue, dérivable?    

Exercice monotonie à partir d\'un certain rang

Exercice monotonie à partir d\'un certain rang

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 14-03-20 à 01:02

Bonjour.

Je vais donc donner une idée de ma solution.
Dans un premier post, je vais exposer des résultats qui se déduisent facilement de ce qu'ont écrit luzak et carpediem.
Dans un deuxième post, je montrerai comment je les utilise pour obtenir le résultat que j'ai annoncé.
A bientôt.

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 14-03-20 à 01:16

A partir des résultats exposés par carpediem et luzak, on peut affirmer ceci:

P1 : Pour tout (a,t), la suite (x_n(a,t))_{n\in\mathbb N} admet une limite, cette limite pouvant être 0,1 ou +\infty.

P2: La suite (x_n(a,t))_{n\in\mathbb N} admet pour limite  +\infty si et seulement si
\exists N \in\mathbb N \ , \ x_N(a,t) > 1

P3: Lorsque la suite (x_n(a,t))_{n\in\mathbb N} n'est pas la suite nulle, la suite (x_n(a,t))_{n\in\mathbb N} admet pour limite 0 si et seulement si:
\exists N\in \mathbb N \ , \  x_{N+1}(a,t) <x_N(a,t)

P4: Pour tout n de \mathbb N et pour tout t, l'application  a\longmapsto x_n(a,t) est continue

P5: Soit t \geq 0 et  a,b deux réels positifs tels que a\leq b.
Alors:   \forall n \in \mathbb N \ , \ x_n(a,t)\leq x_n(b,t).
De plus:    \lim_{n\rightarrow +\infty} x_n(a,t)=+\infty \Longrightarrow \lim_{n\rightarrow +\infty} x_n(b,t)=+\infty
                       \lim_{n\rightarrow +\infty}x_n(b,t)=0 \Longrightarrow \lim_{n\rightarrow +\infty}x_n(a,t)=0

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 14-03-20 à 01:35

J'utilise P1,P2,P3,P4,P5 définis dans le post précédent.

Soit  t \in [0,1[.

Notons:   C_0(t)= \{ a \in ]0,+\infty[ \ | \ \lim_{n\rightarrow +\infty}x_n(a,t)=0\}
                     C_1(t)= \{ a \in ]0,+\infty[ \ | \ \lim_{n\rightarrow +\infty}x_n(a,t)=1\}
                      C_{\infty}(t)= \{ a \in ]0,+\infty[ \ | \ \lim_{n\rightarrow +\infty}x_n(a,t)=+\infty\}

P1 permet d'affirmer que     ]0,+\infty [ = C_0(t)\cup C_1(t)\cup C_{\infty}(t).

C_{\infty}(t) est non vide puisqu'il contient 1
C_0(t) est non vide puisqu'il contient \dfrac{1}{3} lorsque t=0 et \dfrac{t-t^2}{2} lorsque t\in]0,1[.

P5 permet d'affirmer que C_0(t) et C_{\infty}(t) sont deux intervalles.

P3 , P4  et P5 permettent d'affirmer que C_0(t) est ouvert. En effet, si a appartient à C_0(t), il existe N\in \mathbb N tel que  x_{N+1}(a,t) <x_N(a,t). Par continuité, il existe \varepsilon >0 tel que x_{N+1}(a+\varepsilon,t)<x_N(a+\varepsilon,t). Et, d'après P3, a+\varepsilon est dans C_0(t). P5 permet alors d'affirmer que ]0,a+\varepsilon [ est inclus dans C_0(t).

De même, P2 , P4 et P5 permettent d'affirmer que C_{\infty}(t) est ouvert.

Tout ce qui précède permet d'affirmer qu'il existe \alpha et \beta tels que
C_0(t)= ]0,\alpha[       et       C_{\infty}(t) = ]\beta,+\infty[.
Et, par suite      C_1(t) = [\alpha,\beta]

Il reste à montrer que    \alpha = \beta.
Cela fera l'objet du post suivant.

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 14-03-20 à 01:58

Supposons que \alpha \neq \beta et donc que \alpha <\beta .

Puisque (x_n(\alpha ,t))_{n\in\mathbb N} converge vers 1, il existe N\in\mathbb N tel que   \forall n \geq N \ , \ x_n(\alpha ,t) \geq \dfrac{3}{4}
Rappelons que:    \forall n \in \mathbb N^{\star} \ , \ x_n(\beta,t) > x_n(\alpha,t)

Pour n \geq N, on a:
x_{n+1}(\beta,t)-x_{n+1}(\alpha,t) \geq x_n(\beta,t)^2-x_n(\alpha,t)^2 \geq \dfrac{3}{2} \left[ x_n(\beta,t)-x_n(\alpha,t)\right]
x_n(\beta,t)-x_n(\alpha,t) \geq \left(\dfrac{3}{2}\right)^{n-N} \left[x_N(\beta,t)-x_N(\alpha,t)\right]

Et ceci est contradictoire (passer à la limite).

Donc  \alpha =\beta.

CQFD

Posté par
perroquetre : Exercice monotonie à partir d'un certain rang 14-03-20 à 02:07

Merci à XZ19 pour les deux jolis graphiques.

Je pense que \alpha est C^1 mais je ne suis pas très motivé pour en chercher une démonstration.

Posté par
luzakre : Exercice monotonie à partir d'un certain rang 14-03-20 à 09:55

Et merci à perroquet pour ce travail impressionnant et bien détaillé !


Rechercher
Menu
Espace membre
19 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !