Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Exercice Nombre Complexe dans un Plan complexe

Posté par
Mauve 08-10-09 à 10:12

Bonjour,

Je suis devant la deuxième question de mon exercice et je ne comprend pas ce que je dois faire. Pour vous permettre de comprendre, voici l'exercice en entier, et mes réponses au premier numéro.

"Exercice 2"

1) Résoudre dans l'ensemble C des nombres complexes, l'équation : z² -2z + 4 = 0.
Notez z1 la solution dont la partie imaginaire est positive et z2 l'autre solution.

Alors ici je comprend qu'il faut utiliser le discriminant (Delta) = b²-4ac pour trouver la réponse.

Je trouve : (D) = b²-4ac = 2² -4a4 = 4 - 16 = -12 = 12i² ce qui donne aussi (iv-D) et (iv12)²

avec v = racine carrée et d = delta

Comme le discriminant est plus petit que zéro, on a deux solutions complexes non réelles, conjuguées.

z1 = -1+iv3 et z2 = -1 -iv3

2) Dans le plan complexe représenter les points A et B d'affixes respectives z1 et z2.

Alors je fais mon plan et je place A et B; A = -1x +1,75y (environ) et B = -1x -1,75y (environ)

Et la question qui m'embête, la voici :

"C est le point d'affixe -2. Démontrez que le triangle A, B, C est équilatéral."

Pour moi, c'est impossible... un triangle équilatéral possède 3 côtés identiques, et là ça n'est pas le cas...

A = -1 + iv3
B = -1 - iv3
C = -2

VAB= 2iv3
VAC= -1- iv3
VBC= -1 +iv3

(V pour vecteur)

Enfin, c'est surtout que je suis visuelle et que sur l'image, ce triangle là est isocèle et pas équilatéral...

Pourriez-vous m'aider s'il vous plait ?
Merci.

Posté par
ciocciure : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 10:17

salut
à vue de nez je dirais
erreur de signe sur z1 et z2


Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 10:20

Bonjour,
tu as fait une erreur de signe
pour les solutions \frac{-b-\sqrt{\Delta}}{2a} ;\frac{-b+\sqrt{\Delta}}{2a}
z1=1-i√3
et z2=1+i√3

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 11:07

"Notez z1 la solution dont la partie imaginaire est positive et z2 l'autre solution."

Vous êtes certains ? Oo

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 11:44

oui change....

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 11:45

z1=1+i√3
et z[sub]2=1-i√3[/sub]

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 11:46


z1=1+i√3
et z2=1-i√3

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 13:41

Ohlala la bourde xD

Mais alors, c'est que -2/2 ne donne pas -1 ? Désolé, je ne suis pas très douée avec les maths.

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 13:43

Eh ben, en effet là j'ai un triangle équilatéral ! Merci !

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 14:03

z² -2z + 4 = 0.
∆=-12=
√∆=2i√3
b=-2 donc b=2
a=1 donc 2a=2

z_1=\frac{2+2i\sqrt{3}}{2}=1+i\sqrt{3} \\ z_2=\frac{2-2i\sqrt{3}}{2}=1-i\sqrt{3}
C(-2)
z_1=z_A et z_2=z_B \\ |z_A-z_B|=|1+i\sqrt{3}-1+i\sqrt{3}|=2\sqrt{3} \\ |z_A-z_C|=|1+i\sqrt{3}+2|=\sqrt{(1+2)^2+\sqrt{3}^2}=2\sqrt{3} \\ |z_B-z_C|=|1-i\sqrt{3}+2|=2\sqrt{3}

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 14:14

J'avais fait une grosse bêtise, j'avais oublié de mettre des parenthèses à -b alors j'ai gardé "-2" sans réfléchir...

Tout s'explique.

Merci beaucoup !

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 14:19

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 14:46

Il y a un autre numéro de cet exercice qui me pose problème...

"3) À tout point M(z) on fait correspondre le point M' = f(M) d'affixe : z' = z + iv3

a) Déterminez l'affixe D tel que D = f(A) et celle de E tel que f(E) = C.

b) K est le milieu du segment [AC]. Démontrez que D, E, et K sont alignés."

Je ne comprend pas ce qu'il faut faire...

Ils veulent que l'on fasse quelque chose comme D(z) = A(z) ? On aurait quelque chose comme A= D et E=C et on aurait les points DEK alignés puisque k est le milieu du segment [AC] ?

A mon avis ça doit être beaucoup plus compliqués que ça... :s

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 15:13

a)au point M(z)  on associe le point M'(z') ,image de M , par f et f(z)=z'=z+i√3

D = f(A):
on te demande de déterminer l'affixe du point D  ,image de A par f
tu connais l'affixe de A et tu dois déterminer celle de D en appliquant la formule
z_D=z_A+i\sqrt{3} tu finis le calcul

f(E) = C :
tu cherches l'affixe  z du point E ,sachant que son image est le point C  
f(z_E)=2=z_E+i\sqrt{3}
tu résous

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 15:34

Ah, d'accord.

Alors zD = zA +iv3 = 1+2iv3

Et zB + iv3 = 1+iv3

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 15:38

pour ZDOK
pour ZB pourquoi B??
tu dois chercher ZE sachant que
2=zE+i√3

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 15:54

Ohlala, pardon, je voyais un B à la place du E !

Hum...

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 08-10-09 à 16:11

tu termines le calcul
2=zE+i√3
zE=?

Citation :
b) K est le milieu du segment [AC]. Démontrez que D, E, et K sont alignés

z_K=\frac{z_A+z_C}{2}
ensuite pour alignement des points
montre que \frac{z_D-z_E}{z_D-zK} est un réel

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:22

Désolé j'ai du partir hier,

Alors... si 2 = zE +iv3,

zE = 2 - iv3

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:30

OK
relis mon Post le 08-10-09 à 16:11
pour K et alignements des points , ce n'est que du calcul

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:32

Pour montrer que (2D -2E)/(2D-2K) est un réel je tente juste de le résoudre dans C et je m'arrange pour qu'il ne reste que la partie réelle à la fin ?

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:33

Okay, merci je tente ça ^^

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:37

ce n'est pas une équation...
tu remplaces par les affixes des points...
tu simplifies ....
et tu dois obtenir un réel...

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:54

Là j'ai le résultat d'un premier calcul...

Je dois maintenant faire en sorte de retirer la partie imaginaire de ce nombre complexe, en utilisant le conjugué du dénominateur je crois... ^^

Voilà ce que ça donne pour le moment :

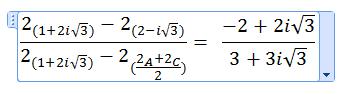
Exercice Nombre Complexe dans un Plan complexe

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 09:59

oui ,et  je vérifie
pour info tu as pris une image de ta calculatrice???

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 10:08

J'ai pris une "impression d'écran" sur un document "Word" où je fais mes calculs que j'ai copier/coller sur "Paint" pour avoir une petite image

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 10:22

sans word mais en latex
\rm z_D=1+2i\sqrt{3} \\ z_E=2-i\sqrt{3} \\ z_K=\frac{1+i\sqrt{3}}{2} \\ \frac{z_D-z_E}{z_D-z_K}=\frac{2(1+2i\sqrt{3}-(2-i\sqrt{3}))}{2(1+2i\sqrt{3})-1+i\sqrt{3}}= \\ \frac{2(-1+3i\sqrt{3})}{1+3i\sqrt{3}}= \\ \frac{2(-1+3i\sqrt{3})\time (1-3i\sqrt{3})}{28}=\frac{13}{14}

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 10:52

plutôt
\frac{13}{7}

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 11:11

a  -zk j'avais inversé les signes

Hum... par contre je ne suis pas encore arrivée au résultat (j'ai du partir faire des courses), je vérifie si j'arrive au même résultat que vous.

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 11:37

Bon, je fais forcément une erreur quelque part mais je ne sais pas où...

D'après vos calculs, j'ai inversé les signes de zk en le gardant entre parenthèses. Mais j'ai du mal à suivre vos calculs...

Voilà ce que moi j'ai fait : (Et je n'ai même pas résolu la fin, parce que j'imagine que de toute façon c'est faux)

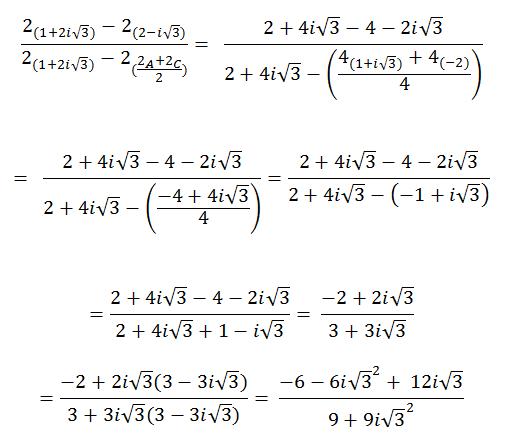
Exercice Nombre Complexe dans un Plan complexe

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 11:49

Si 2iv3 = -12 et (iv3)² = -3 alors j'obtiens -96/-18 moi...

Ensuite reste à faire une plus petite fraction... soit -16/-3

:s

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 13:46

moi aussi je suis partie faire des courses ,,il faut bien remplir le frigo
j'ai fait une erreur de frappe j'ai oublié des parenthèses  pour ZK , ensuite c'est juste


\rm z_D=1+2i\sqrt{3} \\ z_E=2-i\sqrt{3} \\ z_K=\frac{1+i\sqrt{3}}{2} \\ \frac{z_D-z_E}{z_D-z_K}=\frac{2(1+2i\sqrt{3}-(2-i\sqrt{3}))}{2(1+2i\sqrt{3})-(1+i\sqrt{3})}= \\ \frac{2(-1+3i\sqrt{3})}{1+3i\sqrt{3}}= \\ \frac{2(-1+3i\sqrt{3})\time (1-3i\sqrt{3})}{28}=\frac{13}{7}
je ne comprends pas ton calcul pourquoi as-tu 4 au dénominateur??

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 14:35

Eh bien... parce que j'ai fait 2(E) :s

Je me suis dit qu'il fallait faire (2((2A+2C)/(2))) alors ça m'a donné ce qui est à côté ^^'

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 14:58

mais (2((2A+2C)/(2))) =2(A+C)

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 15:01

Ah...

C'est pour ça que j'avais un mauvais résultat alors

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 15:02

oui

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 15:03

Mais je ne comprend pas comment tu passes de 1+3iv3 à 28 en dénominateur

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 15:31

(1+3i√3)(1-3i√3)=1+(32*3)=27+1=28

Posté par
Mauvere : Exercice Nombre Complexe dans un Plan complexe 09-10-09 à 15:36

Ah oui, d'accord ^^

Merci.

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 19:38

bonsoir a tous , j ai le meme exercice mais je suis pas du tout sur de mes reponses
pouvez vous m aider ? svp

j arrive a faire le 1)
z1 = -1+iv3 et z2 = -1 -iv3

mais j arrive pas a faire les autres :S
pouvez vous m aider ? svp

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 19:42

tu retrouves de vieux topics...
je fais manger  le mari ,le chien... et je reviens..

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 19:50

ouai ..
ok pas de probeleme
je vous remercis

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 20:03

erreur de signe
z=\frac{-b\pm\sqrt{\Delta}{2a}

z_1=1+i\sqrt{3}
z_2=1-i\sqrt{3}

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 20:05

z=\frac{-b\pm\sqrt{\Delta}}{2a}

z_1=1+i\sqrt{3} \\ z_2=1-i\sqrt{3}
  
je regarde la suite après le repas

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 20:07

merci

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 20:44

j arrive pas a faire le 2)

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 21:21

Citation :
C est le point d'affixe -2. Démontrez que le triangle A, B, C est équilatéral."

C(-2) \\ z_1=z_A et z_2=z_B \\ |z_A-z_B|=|1+i\sqrt{3}-1+i\sqrt{3}|=2\sqrt{3} \\ |z_A-z_C|=|1+i\sqrt{3}+2|=\sqrt{(1+2)^2+\sqrt{3}^2}=2\sqrt{3} \\ |z_B-z_C|=|1-i\sqrt{3}+2|=2\sqrt{3}

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 21:31

est ce que vous avez fais
module de( za-zb) = module de (ranice (za^2-zb^2) pour trouver 2racine de 3 ?

Posté par
dana94re : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 21:41

je vois pas comment vous faite pour trouver  2racine 3
et pour les autres

Je suis désolée de vous avoir dérangé  
mais pouvez vouz m expliquer

Posté par
Labore : Exercice Nombre Complexe dans un Plan complexe 02-10-11 à 21:45

tu as oublié le cours...
z=x+iy
|z|^2=x^2+y^2
|z|=\sqrt{x^2+y^2}

1 2 +


Rechercher
Menu
Espace membre
22 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1729 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !