- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
(exercice) ntégartion des fonctions à doubles variables
Salut à tous
je suis nouveau sur le site et je trouve dommage de trouver ce site aussi tard.
voilà je fais un cours de calcul intégrale dans l'espace. j'espère avoir bien positionner mon sujet dans le forum. Étant donné que l'exercice est accompagné d'un schéma je vous donne le lien. Il s'agit de la question1.
A l'aide des intégrales multiples, déterminez le volume d'un cône de rayon a et de hauteur H dont on a tronqué le dessus d'une hauteur h.
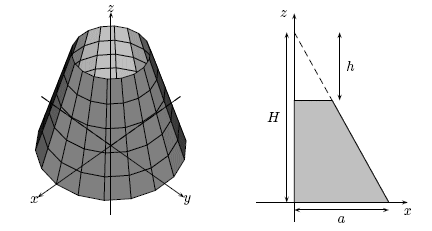
Si vous savez comment résoudre ce problème veuillez me guider, je ne sais pas vraiment par où commencer.
merci d'avance.
Edit Coll : lien effacé ; énoncé recopié ; image postée... merci d'en faire autant la prochaine fois !
Salut.
D'après moi le plus simple (et ce qui me paraît suggéré par la figure de droite), c'est de dire que le volume cherché est l'intégrale pour  variant dans [0,2
variant dans [0,2 [ de l'aire de la figure grise.
[ de l'aire de la figure grise.
Cette aire étant elle-même l'intégrale pour z entre 0 et (H-h) de l'intégrale entre 0 et -az/H+a (ce qui correspond à l'équation de la génératrice du cône) de dxdz.
Donc si V est le volume que tu recherches :
En espérant que je n'aie pas fait d'erreur...


 analyse complexe en post-bac
analyse complexe en post-bac