Inscription / Connexion Nouveau Sujet
Fonction affine
bonjour, je ne comprend pas cette exercice donc je viens demander de l'aide à plus doué que moi ... Merci par avance
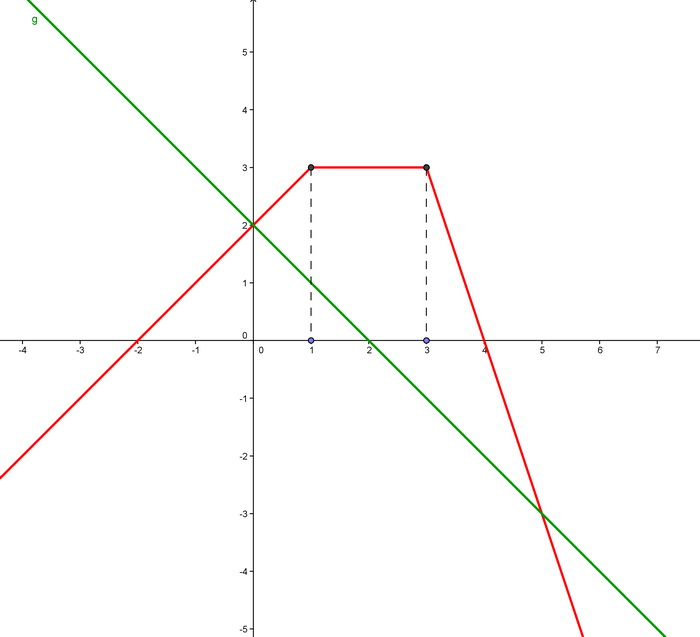
La courbe ci-dessus, tracée dans un repère orthonormé; est celle du fonction f définie sur R.
1. Trouvez les expressions algébriques qui permettent de calculer f(x) suivant les valeurs de x.
2. g est la fonction définie sur R par g(x)= 2- x.
a)Tracer la droite représentative de g sur le graphique.
b)Graphiquement, précisez le nombre de solutions de l'équation f(x)=g(x)
Bonjour alex231
Il s'agit de trouver les équations des trois segments de droites en déterminant les équations des 3 droites.
La 1ère droite passe par les points A de coordonnées (-2 ;0) et B de coordonnées (1 ;3).
Tu peux en trouver l'équation…
Cette équation est de la forme y = mx + p où le coefficient directeur m se calcule par la formule
Le calcul de p se fera ensuite en exprimant que le point A appartient à la droite.
N.B. : On peut deviner cette valeur de p par le point d'intersection de la droite avec l'axe des ordonnées.
Reprenons autrement.
L'équation d'une droite non parallèle à l'axe des ordonnées est de la forme : y = mx + p.
La 1ère droite passe par les points A de coordonnées (-2 ;0) et B de coordonnées (1 ;3).
Pour exprimer que A(-2 ;0) appartient à cette droite , nous pouvons remplacer x par -2 et y par 0 dans l'équation y = mx + p.
Nous avons : 0 = -2m + p.
Même chose pour B(1 ;3).
Nous avons : 3 = m + p.
Il nous reste à résoudre le système :
.
En soustrayant la 1ère equation de la 2ème, on a :
(m + p) - (-2m + p) = 3 - 0.
m + p + 2m - p = 3.
3m = 3
m = 1.
Remplaçons m par 1 dans la 1ère équation :
-2*1 + p = 0
-2 + p = 0
p = 2.
On a ainsi trouvé que m = 1 et p = 2.
L'équation de la 1ère droite est alors : y = x + 2.
Tu peux faire le même raisonnement pour les deux autres droites ?
Merci beaucoup, j'ai compris 
Maintenant si vous pouviez juste m'expliquer comment m'y prendre pour la question 2, si cela ne vous dérange pas, sa serais super gentils, merci 
Je suppose que tu as trouvé ceci pour la question 1.
.
Pour la question 2) a), je suppose que tu peux représenter la droite en donnant à x deux valeurs distinctes et en calculant leurs images.
Le nombre de solutions de l'équation f(x) = g(x) sera déterminé par le nombre de points d'intersection entre les graphiques représentant les deux fonctions f et g.
Pouvez vous s'il vous plait détaillé les calculs pour la droite 2 et 3 de la question 1 pour que je trouve mon erreur ... Je n'ai pas trouver comme vous .. :/
Droite 2 : m + p = 3
3m + p = 3
déja on voit qu'il y a forcement une erreur ... mais je n'arrive pas a voir comment la résoudre
Droite 3 : 3m + p = 3
4m + p = 0
Mais c'est parfait !
Droite 2 : Tu soustrais les deux équations entre elles.
(3m + p) - (m + p) = 3 - 3.
3m + p - m - p = 0.
3m = 0.
m = 0.
Tu remplaces m par 0 dans la 1ère équation.
0 + p = 3.
p = 3.
On a ainsi trouvé que m = 0 et p = 3.
L'équation de la droite D2 est alors : y = 0x + 3, soit y = 3.
Droite 3 : Tu soustrais les deux équations entre elles.
(4m + p) - (3m + p) = 0 - 3.
4m + p - 3m - p = -3.
m = -3.
Tu remplaces m par -3 dans la 1ère équation.
3*(-3) + p = 3.
-9 + p = 3.
p = 3 + 9.
p = 12.
On a ainsi trouvé que m = -3 et p = 12.
L'équation de la droite D3 est alors : y = -3x + 12.
Super, je coyais avoir faux, bon cela montre que sa c'est acquis ... Alors maintenant je suis sur la question 2 et j'qi du mal a tracer la droiterepresentative de g ... Les points je ne peux pas les choisies aux hasards ...
Appelons D4 la droite représentant la fonction g.
g(x) = 2 - x.
Donnons à x deux valeurs au hasard.
Si x = 0, alors g(x) = 2 - 0 = 2. Le point de coordonnées (0 ;2) appartient à la droite D4.
Si x = 2, alors g(x) = 2 - 2 = 0. Le point de coordonnées (2 :0) appartient à la droite D4.
Tu peux alors tracer la droite D4 passant par ces points…
Ah merci beaucoup pour tout le mal que vous vous donnez, de votre graphique je déduit qu'il y a 2 solution pour f(x) = g(x) , ce sont les moments ou ls droites se croisent, c'est justes ? 
Bonjour excuser moi de vois déranger mais j'ai le même problème. Je ne comprends pas la question 2)b ainsi que la 3) et je voudrais savoir si on peut vraiment utiliser des nombre au hasard pour la question 2)a s'il vous plait. Merci 
Bonjour Brillancya
je voudrais savoir si on peut vraiment utiliser des nombre au hasard pour la question 2)a
Il n'est pas écrit que nous avons choisi deux points au hasard dans le plan.
Il est écrit ceci :
Appelons D4 la droite représentant la fonction g.
g(x) = 2 - x.
Donnons à x deux valeurs au hasard.
En effet, une méthode pour construire une droite consiste à connaître deux de ses points.
En donnant à x deux valeurs au hasard, nous choisissons les abscisses de ces deux points.
Puis nous calculons les ordonnées correspondantes en utilisant l'expression de g(x).
C'est bien ce qui a été décrit dans le message du 21-12-10 à 18:56.
Si x = 0, alors g(x) = 2 - 0 = 2. Le point de coordonnées (0 ;2) appartient à la droite D4.
Si x = 2, alors g(x) = 2 - 2 = 0. Le point de coordonnées (2 :0) appartient à la droite D4.
Tu peux alors tracer la droite D4 passant par ces points…