- Fonctions sinus et cosinus
- Exercice sur les fonctions Sinus et Cosinus
- Variations autour des fonctions sinus et cosinus
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Fonction cosinus
Bonjour à tous, j'ai un exercice à faire mais je bloque dessus, pouvez vous m'aider svp ?
Exercice :
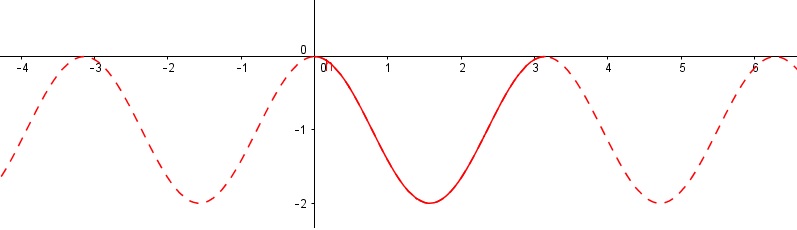
Soit f la fonction définie sur R par f(x)=cos(2x)-1.
Après avoir étudier les variations de la fonction f, tracer dans un repéré sa courbe représentative.
J'ai trouvé f'(x)=-2sin(2x) mais après je suis bloquée.. J'ai pensé à faire un encadrement mais je ne voit pas comment faire pour passer de
-1 < sin x < 1 à ? < -2sin(2x) < ?
tu pourrais avant tout étudier la parité et la périodicité de ta fonction pour pouvoir diminuer l'intervalle sur lequel tu étudieras les variations de f
Bonjour,
Ce que tu dit bbjhakan, c'est de diminuer ton domaine d'étude par le biais de l'étude de la parité et de la périodicité de ta fonction.
bonsoir Jedoniezh!
as-tu vu en cours l'étude de la parité en calculant et l'étude de la périodicité?
Ou tu n'as pas retenu le nom.
Donc ta fonction présentement, elle paire ou impaire ou ni l'une ni l'autre ?
Si j'ai bien compris, ma périodicité est de 2 car on sait que xE[0;π] et on cherche 2xE[?;?]. C'est ça ?
Ah je comprend mieux.. Mais du coup la périodicité et savoir que la fonction est paire va nous apporter quoi ?
que la fonction est paire va nous apporter quoi ?
A réduire ton domaine à [0;+
 [ (vu à 19:38)
[ (vu à 19:38)
du coup la périodicité va nous apporter quoi ?
A la même chose, à réduire ton domaine d'étude (dit à 19:14)
Non, une fois qu'on a fait cela (si je comprends ce que tu veux dire par "cela"), on réduit le domaine d'étude.
Est ce que c'est juste ?
Non.
Mais le domaine d'étude est déjà réduit à [0;+
 ] non ?
] non ?Oui, grâce à l'étude de la parité.
Maintenant, il faut le réduire encore grâce à l'étude de la périodicité.
Et du coup, là on doit dire que
cos'(2x)-1 = -2sin(2x)
or, sin x > 0 sur [0;π] donc cos'(2x)-1 < 0
La fonction cosinus est décroissante sur [0;π]
Et après on construit le tableau de variation, est-ce juste ?
et du coup on rajoute π/2 entre 0 et + dans la premiere ligne du tableau. De même dans la troisième ligne en dessus de π/2 on met f(π/2)=-1 ?
dans la premiere ligne du tableau. De même dans la troisième ligne en dessus de π/2 on met f(π/2)=-1 ?
La deuxieme ligne est elle juste ?
et du coup on rajoute π/2 entre 0 et + dans la premiere ligne du tableau. <== non, on fait un tableau entre 0 et
dans la premiere ligne du tableau. <== non, on fait un tableau entre 0 et 
Ah oui bien sur, j'avais oublier qu'on avais reduit une deuxieme fois mais sinon on met bien π/2 entre les deux ? et tout ce que j'ai dit avant
Merci pour l'aide, ensuite j'ai juste à tracer la courbe dans un repère ce qui devrais être assez facile.. Merci beaucoup pour l'aide, j'ai réussi à comprendre des choses que je n'avais pas compris 

 (flèche qui va vers le haut)
(flèche qui va vers le haut)