Inscription / Connexion Nouveau Sujet
Fonction inverse#Exercice
Bonjour (;
Classe#Seconde
Matière#Mathématiques
Enoncé exact:
Les trois fonctions suivantes ont été représentées sur le graphique ci-dessous
f:x->x² g:x->x h:x->1/x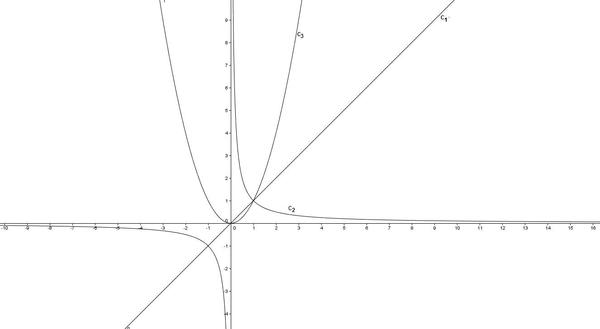
1)Attribuez à chaque fonction sa représentation graphique.Justifiez votre réponse.
2)On souhaite ranger dans l'ordre croissant les trois nombres x;x² et 1/x en distinguant quatre cas.
Rangement:
1e cas : x≤ -1 .........
2e cas -1≤x<0 1/x≤ x≤ x²
3e cas:... ........
4e cas: ... .........
Mes réponses:
1) f:x→x² est une fonction carré car la fonction carré est la fonction f:x→x².
De plus un fonction carrée est : - croissante sur [0;+∞[
- décroissante sur ]-∞;0]
-représente une parabole
Donc f:x→x² est représenté par la courbe C3
g:x→x
Pour celle là je sais que c'est la courbe C1 mais je ne sais pas justifier...
h:x→1/x est une fonction inverse car on appelle fonction inverse la fonction f définie par f:x→1/x pour tout x appartenant à R.
De plus elle est représentée par une hyperbole.
Donc h:x→1/x est représentée par la courbe C2.
2) Là je n'ai rien compris...
Merci (;
Bonjour
pour y=x, c'est une fonction linéaire d'où une droite...
pour la 2
mets toi d'abord à gauche de -1
(sur l'axe des abscisses)
et lis sur le dessin les ordonnées sur chacune des courbes
cela te donne 1/x ; x et x², que tu peux comparer puisque tu sais qui est en dessous de qui....
1) g:x -> x, c'est une droite
2) En gros, ici, tu dois couper R en 4 domaines (les 2 premiers te sont donnés) où x, x2 et 1/x sont "dans le même ordre".
Exemple qui t'es donné (cas 2) : entre -1 et 0, tu peux voir sur le graphe que 1/x est toujours inférieur à x qui lui-même est toujours inférieur à x2. On a donc 1/x <= x <= x2
A toi de trouver les 2 domaines restants et "l'ordre" des fonctions sur chaque domaine. 
Merci d'avoir répondus (;
Pour la 1) g:x→x je dois justifier. Je ne doit pas me contenter de juste dire: c'est une droite :$
@malou: Je ne me souviens pas avoir appris que y=x...Peut-être que j'ai une mémoire de poisson ^^
2)
@Malou: Je n'ai pas très bien compris votre technique.
Je me met à gauche de -1, ok. Mais ensuite je vois pas comment je dois lire les ordonnés :$ Ordonnées de -1 ?
@brubru: J'ai du mal aussi..Je suis vraiment bête.
Pour le cas 1. x≤ -1
Donc x est dans l'intervalle ]-infini; -1] mais après je ne sais pas lequel est plus petit que...
Merci
alors g(x)=x fonction linéaire, cela fait partie du programme de 3e, donc c'est considéré comme acquis, et tu as le droit de t'en servir
je reprends l'explication
tu prends la droite d'équation x=-2 par exemple
fais le dessin sur ton papier
cette droit (parallèle à l'axe des ordonnées) coupe de "bas en haut" la droite, l'hyperbole puis la parabole
donc g(-2) < h(-2) < f(-2)
et je sais donc comparer les images de -2 par g, h et f
voilà, là c'est un exemple (x=-2), et tu fais la même chose pour x entre - l'infini et -1; etc....
Ok je vais essayer alors (;
Juste ce que je ne comprend pas c'est:
J'ai tracer la droite d'équation x=-2
Maitenant quand je regarde qui est coupé en 1er moi je voit: h(-2)<g(-2)<f(-2) et non g(-2)<h(-2)<f(-2)...
oh!...
ta droite rouge (x=-2) coupe d'abord la droite (et pas l'hyperbole) donc c'est g(-2) d'abord...(le plus bas..;donc le plus petit)
ça va ? ou bien il y a quelque chose que tu ne comprends pas...
Ah il me semble avoir compris !!
Je me suis trompé pour -2 en effet l'hyperbole h est plus grand que C1 ( g ) ^^
Bon j'essaie pour les autres.
1er cas: x≤-1 -----------g≤h≤f soit x≤1/x≤x²
2ème cas ( déjà donnée)
3ème cas: On a fait x plus petit que -1 et x entre -1 et 0 donc maintenant la logique serait de faire x compris entre 0 et 1.
0≤x≤1--------------f<g<h soit x²≤x≤1/x
4ème cas: x≥1------------h≤g≤f soit 1/x≤x≤x²
Je pense avoir compris ^^
Donc pour la 1. Je dit que g:x→x est une fonction affine. La fonction g est donc représentée par une droite qui passe par l'origine.
c'est ça ! tu as compris
pour la 1 aussi, affine, donc droite, et ici b=0, donc passe par l'origine, c'est bien ça !
Ah merci beaucoup (; C'est tous simple au final 
Ps: J'ai un autre problème pour une représentation graphique mais j'ai compris qu'un topic= un exercice donc je vais ouvrir une nouvelle discussion (;
Merci encore à vous deux.
Biz.


