Inscription / Connexion Nouveau Sujet
fonctions réciproques ! GROS PROBLEME !
Bonjour,
J'ai un exercice de maths à faire mais je ne comprends vraiment rien à l'énoncé !


on a f (x )=(x-20)²-4
On nous demande quelle est l'image de la réciproquee f-1(]-4,0[) de l'intervalle ]-4,0[ ?
Pouvez vous m'aider s'il vous plaît ?Merci beaucoup !
bonjour;
Pour q'une fonction f admet une réciproque sur un intervalle ]a,b[,donnée.Il faut qu'elle soit continue et strictement monotone sur cet intervalle.
La fonction que vous présenter est définie sur R et elle continue sur son Df(fonction polynôme)et on lui a attribué une fonction réciproque sur un intervalle(
que l'on cherche)
on sait que; f(x)=y <==> f^(-1)(y)=x
alors;f^(-1)(]-4,0 [) = I (un intervalle)
de même; f(I)=]-4,0[
à la limite des conditions sitées(dessus) on peut faire;
I=]A,B[ tel que f(A)=-4 et f(B)=0
(A-20)^2-4=-4 ==> A = 20
(B-20)^2-4=0 ==> b = 22
finalement,I=]20,22[ c'est ce que vous cherchez.
Bonjour
Je te propose deux solutions
La premiére :
On sait que si y=f(x) alors
Ici on demande de déterminer x pour
donc ..........
La deuxiéme :
On calcul cette application réciproque mais cela risque d'etre un peu plus long ...
P-S , auparavant je te proposerais de démontrer que f est bijective sur ]-4;0[ ...

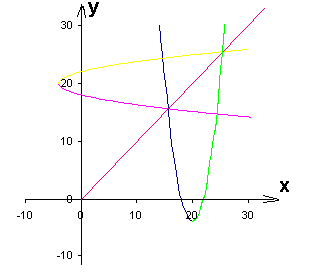
f(x) a pour courbe la courbe bleue et verte.
Son inverse lui est symétrique par rapport à la première bissectrice des axes (en rouge)
On obtient la courbe mauve et jaune.
Par calculs.
f(x)=(x-20)²-4
y = (x-20)²-4
On croise les lettres x et y
x = (y-20)² - 4
on essaie de mettre sous forme y = ...
(y - 20)² = x + 4
y -20 = +/- V(x+4) èV pour racine carrée).
y = 20 +/- V(x+4)
Le + correspond à la partie jaune de la courbe.
Le - correspond à la partie mauve de la courbe.
Comme il s'agit d'une fonction, on ne peut prendre en considération que soit la courbe en jaune, soit celle en mauve et de plus limitée dans un certain intervalle.
Mais il reste un doute dans mon esprit, pour décider quelle partie choisir à partir de l'énoncé et je préfère ne pas en dire plus.
-----
Sauf distraction. 
Je viens de voir les autres réponses en envoyant la mienne, je continue à penser qu'il n'est pas évident de savoir si on doit considèrer f(x) sur ]18 ; 20[ ou sur ]20 ; 22[

excellent travail cette courbe ! 
Peut-etre que l'exercice vise a considerer les deux intervalles l'un apres l'autre.



 analyse en post-bac
analyse en post-bac