Inscription / Connexion Nouveau Sujet
groupe quotient
bonjour à tous
j'ai passé 4 heures hier soir à méditer sur la partie des groupes quotients et je n'arrive toujours pas à comprendre ce que c'est!!
est ce que les éléments de n'importe quel groupe quotienté par un de ses sous-groupes sont des classes d'équivalences? (comme c'est le cas pour ) mon principal problème est de déterminer les élements qui forment ce groupe.
sinon je bloque sur quelques exos et j'ai quelques questions à poser. je dois montrer que G/N abélien D(G)
N sachant que N est distingué dans G , que D(G) c'est le groupe dérivé de G (le sous groupe engendré par l'ensemble des commutateurs de G) . je bloque dans les deux sens de l'équivalence puisque je n'arrivais pas à "voir" quels sont les élements de G/N et ainsi savoir ce qu'il faut faire.
même problème pour trouver un isomorphisme entre avec H un sous groupe distingué dans G et
un automorphisme, impossible de trouver un isomorphisme puisque je ne sais pas sous quelle forme s'écrivent les éléments de ces groupes!
et une dernière petite question, je prend H un ss-groupe distingué dans G , et n son indice , je prend un et je veux montrer que
. je me suis dit que comme H est distingué, il me suffisait d'écrire
sous forme de
avec b dans H, mais je tourne en rond puisque
et ça ne donne rien! puis j'ai voulu utiliser Lagrange, en prenant m l'ordre de G et k celui de H, on aura donc:
m=nk , comme avec e l'élement neutre de G je me suis dit que ça pouvait me faire sortir d'affire mais là encore ça ne me donne rien! ce que j'ai remarqué c'est que je n'ai pas utilisé le fait que n soit l'indice de H, et franchement, je n'ai pas compris le sens de l'exercice.
s'il y a des idées, elles sont les bienvenues 
mercii d'avance et bonne journée
En théorie on peut "quotienter" par n'importe quel sous-groupe, seulement en pratique cela n'a d'intérêt que pour les sous-groupes distingués sinon le quotient n'a plus de structure de groupe.
Pour te donner une idée de ce qu'est un quotient dans le cas simple de Z/nZ, prenons le cas trivial de Z/2Z. Et bien il contient deux élément : {2n; n} et {2n+1; n
} i.e. deux ensembles : le premiers contenant les nombres pairs, le second les nombres impairs.
En fait une classe d'équivalence est un ensemble contenant les éléments qui sont équivalents entre eux.
Alors pourquoi, dans mon exemple, la structure de groupe est-elle respecté ? Car (mis à part que l'ensemble est non vide) déjà on peut définir correctement la notion de somme : ajouter deux nombres pairs ou deux nombres impairs donne un nombre pair. Et ajouter un nombre pair avec un nombre impair donne un nombre impair. Ainsi, si tu prends n'importe quel représentant des classes d'équivalence que tu souhaites ajouter et bien tu tomberas sur un représentant de la classe somme.
Ensuite l'inverse (ici opposé) de la classe des nombres pairs est la classe des nombres pairs et l'opposé de la classe des nombres impairs est la classe des nombres impairs.
On vérifie aisément l'associativité.
Pour compléter mon propos et pour t'aider dans ta démonstration sur G/N abélien, en général ce genre de démonstration se font en choisissant un représentant des classes que tu souhaites multiplier. Ainsi si x est un représentant de X et y un représent de la classe Y. il faut que tu montres que xy sera dans la même classe que yx pour montrer que G/N est abélien. La solution doit être maintenant plus facile...
ok je vois mieux maintenant ce qu'il faut faire. merci kilébo!
et par la même occasion 
Salut izaabelle. Est-ce qu'avant tout tu as bien compris ce qu'est un ensemble quotient (sans parler de groupe) ?
izaabelle,
Si tu as l'occasion de lire le Tauvel Algèbre, il donne une démonstration pour la condition nécessaire et suffisante pour que G/N soit muni d'une structure de groupe. Il donne aussi une démonstration de ton exo...
merci beaucoup pour ces explications.
moi, comment je voyais les choses pour les groupes quotients, c'était qu'on rassemble les éléments du "même type" (qui sont en relation) dans un même ensemble appelé classe d'équivalence.
j'ai une autre question, en haut stokastik, tu as défini la relation d'équivalence comme étant (c'est cette relation même qu'on a définie en cours) mais on peut toujours définir n'importe quelle autre relation d'équivalence R et quotienter par R ??
Je ne suis pas sûr de comprendre ta question.
Si R est une relation d'équivalence sur un ensemble E (sans qu'il n'y ait de groupe ni de sous-groupe en jeu), on peut toujours définir l'ensemble quotient noté E/R, ensemble des classes d'équivalence. Le cas des groupes quotient est un cas particulier.
Ca répond à ta question ?
moi, comment je voyais les choses pour les groupes quotients, c'était qu'on rassemble les éléments du "même type" (qui sont en relation) dans un même ensemble appelé classe d'équivalence.
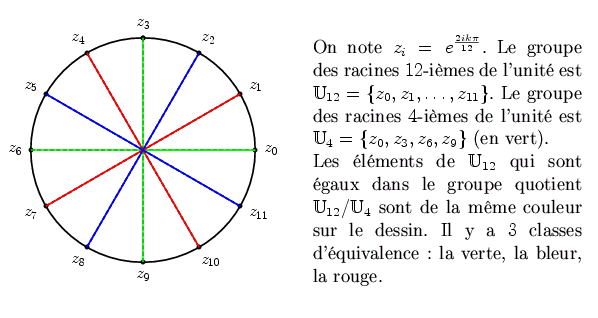
C'est bien cela. Prends mon exemple avec le groupe des racines 12-ièmes de l'unité. Considère la classe rouge {z1, z4, z7, z10}. Ses éléments forment une classe car chacun d'eux est en relation avec l'autre, chacun d'eux est multiple de l'autre par une racine 4-ième de l'unité.
effectivement stokastik, tu as répondu à ma question.
encore merci et bonne soirée 



 algèbre en post-bac
algèbre en post-bac