- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
image d'un cercle par une homographie
bonjour, je suis en 3ème année de licence et je bloque sur un exercice.
Déterminer l'image de l'intersection des deux disques |z-1|<racine(2) et |z+1|<racine(2) par rapport à l'homographie w = (z-i)/(z+1).
Je pense que l'intersection des deux disques est la droite des reels.
Mais pour l'image je ne vois pas du tout comment faire.
Merci de votre aide.
merci je comprends par rapport au dessin.Mais par le calcul je ne vois pas comment on trouve l'image des disques.Et je viens de me rendre compte que w=(z-i)/(z+i).Excusez moi pour l'erreur.
Alors évidemment, c' est autre chose. En général, l' image d' un cercle par un homographie est un cercle où une droite.
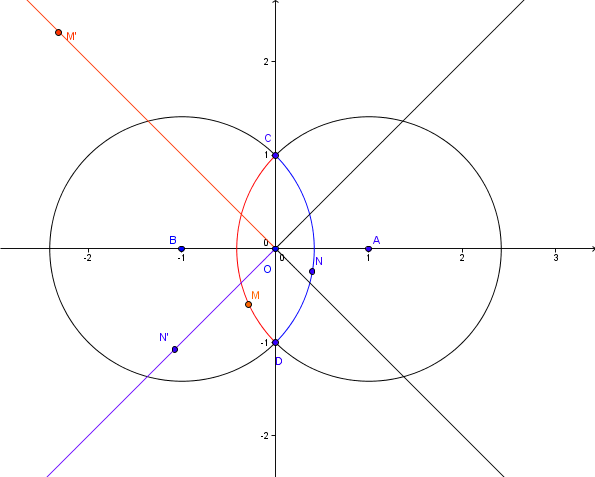
Ici, il s' agit de droites ou plus exactement de demi droites.
Donc il est beaucoup plus rentable de passer par les arguments:
Avec :
Si appartient à l' arc
privé de
du cercle de centre
et de rayon
, alors:
Ce qui nous donne la demi droite issue de en rouge.
Si appartient à l' arc
privé de
du cercle de centre
et de rayon
, alors:
Ce qui nous donne la demi droite issue de en bleu.
L' image du domaine limité par les deux arcs sera le domaine limité par les deux demi droites (à gauche sur la figure).


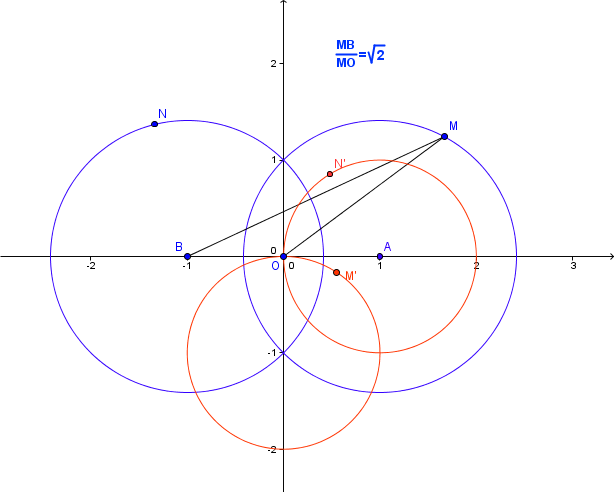

 analyse complexe en post-bac
analyse complexe en post-bac